Wat zijn de uitgangspunten van een OLS-regressie?
Een Ordinary Leas Square (OLS) regressie gaat er van uit dat alle relevante onafhankelijke variabelen zijn opgenomen in je model (regressiemodel / model specificatie) (Best et al., 2014, p. 67). Dit is ook wel bekend als de Best Linear Unbiased Estimates (BLUE) aanname (Best et al., 2014, p. 67). Hiermee bedoelen we dat elke “relevante” variabele die een invloed kan hebben op je afhankelijke variabele is opgenomen in je model. Hoe kom je achter deze variabelen? Dat is een kwestie van veel wetenschappelijke artikelen lezen over jouw specifieke onderwerp/ afhankelijke variabele.
Welke type (lineaire) regressieanalyses kunnen we onderscheiden?
Binnen de familie van regressieanalyses kunnen we heel veel varianten onderscheiden. Zo heb je een enkelvoudige (lineaire) regressie waarbij je kijk van een onafhankelijke variabele op een afhankelijke variabele. Met andere woorden variabele A beïnvloed variabele B. Maar, zoals hierboven al beschreven is, voldoe je dan niet aan de BLUE aannames en zit er waarschijnlijk een sterke miswijzing (Bias) in je resultaten. Daarnaast, kunnen we ook de afhankelijke (criterion) variabele voorspellen met meer dan een onafhankelijke (predictor) variabele. Op het moment dat je meer dan een onafhankelijke variabele (voorspeller) gebruikt spreken we van een meervoudige (lineaire) regressie. Naast deze grove indeling op basis van het aantal opgenomen variabelen, kunnen regressies ook worden onderscheiden op basis van hoe ze omgaan met de relatie tussen onafhankelijke en afhankelijke variabele. Zo zijn er gespecialiseerde regressies mogelijk in SPSS of Stata voor afhankelijke variabelen met een binaire, ordinale of tel (count) eigenschappen.
Waarom is het zo belangrijk dat alle relevante verklarende variabelen zijn opgenomen in je model?
Daar is een eenvoudige reden voor: een regressieanalyse baseert de regressiecoëfficiënten op basis van de gewogen invloed van de andere variabelen in je regressiemodel. Met andere woorden, een regressie is een conditionele analyse (Thompson, 2006). Als je een variabele toevoegt wordt de gemeenschappelijke variatie (overlap) tussen de variabelen verwijderd. Hierdoor worden de variabelen “gezuiverd” van de gemeenschappelijke variatie. Als gevolg meet je dus het unieke effect van een variabele. Daarom, veranderen de regressiecoëfficiënten als je variabelen toevoegt of verwijdert. Dit zuiverende of corrigerende effect van de variabele is een onderdeel van de BLUE aanname. Dit geldt niet alleen voor variabelen die een correlatie met de afhankelijke variabele hebben. Een suppressor variabele heeft bijvoorbeeld geen correlatie met de afhankelijke variabele maar wel met andere onafhankelijke variabele(n) (Thompson, 2006, pp. 237).
Waarom is een suppressor variabele relevant?
Een suppressor variabele “zuivert” de variatie van andere onafhankelijke variabelen waardoor de verklarende waarde van je model kan toenemen. Daarnaast kan de suppressor variabele ook de effect size van de variabelen die hij beïnvloed laten toenemen (Walker, 2003; Thompson, 2006, pp. 237). Dus, zelfs als een onafhankelijke variabele geen significant effect heeft op je afhankelijke variabel, kan deze variabele nog steeds een “zuiverend effect” hebben op een andere variabele. Maar, het mes snijdt aan twee kanten. Een suppressor variabele kan ook zorgen voor multicollineariteit en onstabiliteit in je regressiemodel (Kidwell & Brown, 1982). ). Kortom, een suppressor variabele heeft voordelen en nadelen. Daarom wil je wel de “zuiverende” effecten van een suppressor variabele maar niet de multicollineariteitseffecten.
Wat is confounding variable bias in een regressie?
Dit “zuiverende effect” is tevens van belang om de miswijzing (bias) van je regressie te verminderen. Het weglaten van relevante (confounding) variabelen is in de literatuur ook bekend onder de term Omitted Variable Bias. Deze Omitted Variable Bias zorgt ervoor dat je regressie model onder-gespecificeerd (underfitting a model) is. In niet experimentele data is het vrijwel onmogelijk om alle relevante confounders mee te nemen in je model (York, 2018), desondanks moet de intentie zijn om alle relevante variabele in het model op te nemen.
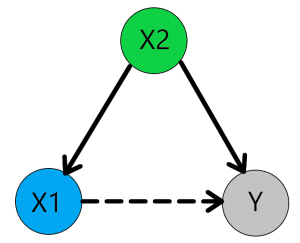
Waarom zijn confounding variabelen belangrijk?
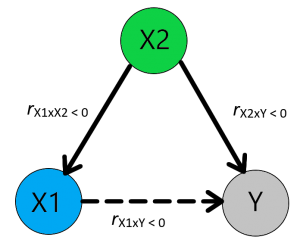
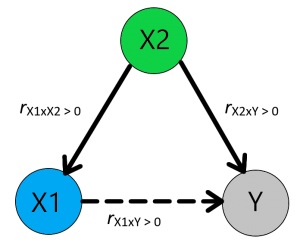
Simpel gezegd, het weglaten van een relevante variabele kan leiden tot een onterechte relatie. Hiermee wordt bedoeld: als we een significantie regressie coëfficiënt vinden tussen een onafhankelijke (X1) en afhankelijke variabele (Y), maar we hebben niet gecontroleerd voor relevante andere (confounder) variabelen (X2), kan deze significante relatie onterecht zijn. De onafhankelijke variabele en afhankelijke variabel kunnen namelijk beide worden beïnvloed door een derde niet geobserveerde confounder (X2). Deze confounder (X2) kan er voor zorgen dat de onafhankelijke (X1) en afhankelijke (Y) groter worden in een bepaalde situatie. Dan lijkt het alsof de onafhankelijke variabele (X1) de afhankelijke variabele (Y) beïnvloed, maar de verandering in de onafhankelijke (X1) en de verandering in afhankelijke (Y) worden dan veroorzaakt door confounder (X2). Hierdoor kan je schatting van het effect van de onafhankelijke (X1) op de afhankelijke (Y) een afwijken van het “echte” effect (Gujarati, 2011, pp. 114-120).
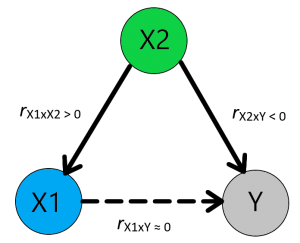
Een mogelijke oorzaak van geen effect tussen X1 en Y
Aan de andere kant, als de confounder (X2) een negatief effect op je onafhankelijke variabele (X1) en een positief effect heeft op je afhankelijke variabele (Y) zou het kunnen voorkomen dat je geen effect meet tussen de onafhankelijke variabele (X1) en afhankelijke variabele (Y). Kortom, om het “echte” effect tussen X1 en Y te kunnen aantonen is het noodzakelijk om voor alle andere beïnvloedende factoren te controleren.
Indien je te maken hebt met confounding variable bias is het onverstandig om meer data te verzamelen, het toevoegen van extra cases lost namelijk het inherente probleem van het ontbreken van relevante variabelen niet op, in deze gevallen is er niet alleen een bias in het model maar is deze ook niet consistent (Gujarati, 2011, pp. 114-120). Om te kunnen controleren of er confounding variable bias aanwezig is kan je een Ramsey’s RESET test uitvoeren (Gujarati, 2011).
Hoeveel controle variabelen zijn er nodig?
Het aantal controle variabelen (confounders) is een dilemma. Je wil voorkomen dan je model onder-gespecificeerd (underfitting a model), maar een over-gespecificeerd (overfitting a model) is ook een probleem. Als je te veel controle variabele meeneemt loop je het risico dat je model de random error weergeeft. Deze random error kan een bijverschijnsel zijn van de unieke eigenschappen van jouw dataset. En geeft dan niet een structureel patroon in de populatie weer maar de toevallige samenstelling van jouw database. En beperkt dus de generalisatie van jouw model naar de populatie. Daarnaast is er een beperking in het aantal variabelen dat je dataset aan kan.
Wat bepaald het maximale aantal variabelen wat mijn dataset aan kan?
Het maximumaantal variabelen hangt af van de combinatie van steekproef omvang (sample size), de kleinste verschillen die je wil detecteren (effect size), de kans op een type I fout (α) en de kans op een type II fout (β). Deze vier factoren bepalen de “power” van je statistische analyse. Statistische power is de kans dan je een effect vindt in je data, op de voorwaarde dat het effect ook daadwerkelijk in je data zit.
Als je meer wil weten hoe je het maximale aantal (controle) variabelen bepaald? Bekijk dan even onze pagina “Hoeveel regressie variabelen kan mijn dataset aan?” voor gedetailleerde informatie.
Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.
Literatuurlijst:
- Best, H., & Wolf, C. (2014). The SAGE handbook of regression analysis and causal inference. Thousand Oaks, California: SAGE Publications.
- Cohen, J. (1988). Statistical Power analysis for the behavioral sciences (2 ed.). New York: Lawrence Erlbaum Associates.
- Gujarati, D. (2011). Econometrics by example. Basingstoke, United Kingdom: Palgrave Macmillan.
- Thompson, B. (2006). Foundations of behavioral statistics: An insight-based approach. New York: Guilford Publications.
- York, R. (2018). Control variables and causal inference: a question of balance. International Journal of Social Research Methodology, 21(6), 675-684.
- Walker, D. A. (2003). Suppressor variable(s) importance within a regression model: An example of salary compression from career services. Journal of College Student Development, 44(1).