De berekening en interpretatie van de Cronbach's alpha uitgelegd en toegelicht.

De Cronbach’s alpha is een van de veel gebruikte testen om aan te tonen of meerdere Likert schaal vragen beschouwd mogen worden als een schaal. Dit gebruik je vaak als je meerdere vragen hebt gesteld in je enquête om een specifiek theoretisch construct te meten. De Cronbach’s alpha wordt vaak ook beschouwd als een betrouwbaarheidsanalyse van de geoperationaliseerde theoretische constructen. De formule van de waarmee je de Cronbach’s alpha kan berekenen is (Cronbach, 1951):

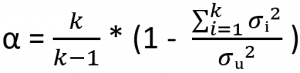
Hierbij is:

k    het aantal enquêtevragen/items welke je wil samenvoegen
σᵢ² de variantie van item _i

σᵤ² de variantie van de totale schaal.

Hoe bereken je de Cronbach’s alpha handmatig?

Een praktisch voorbeeld van de berekening van de Cronbach’s alpha in Excel. Stel dat je vijf vragen hebt gesteld om een bepaalde eigenschap van je respondenten te meten. In ons voorbeeld gaan we er van uit dat 20 respondenten je vragen hebben ingevuld.

Het eerste deel van de Cronbach’s alpha formule

Dan is het eerste gedeelte van de formule   gelijk aan . Dit deel van de formule laat zien dat als het aantal vragen toeneemt, deze correctiefactor lager wordt, en daarmee je Cronbach’s alpha lager wordt. Want als je bijvoorbeeld 10 vragen stelt wordt deze correctiefactor  dus .

Het tweede deel van de Cronbach’s alpha formule

Het tweede gedeelte van de formule is even wat meer werk. Eerst moet de σᵢ² variantie per enquêtevraag /item worden berekend. De variantie σᵢ² kan je handmatig bereken met onderstaande formule, maar je kan natuurlijk ook met het “VAR.S” commando in Excel het in een keer berekenen. Let op dat je hier de variatie berekend van een sample en niet van de totale populatie.

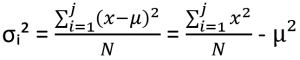
Waarbij, x de waarde van de likertschaal score van respondent i op vraag Q1 is en μ het gemiddelde van alle antwoorden van alle respondenten op vraag Q1 is. Deze variantie wordt ook voor de andere vragen berekend. In dit voorbeeld gebruiken we een 7-punts Likert-schaal omdat recente literatuur aangeeft dat een 7-punts Likert-schaal de grootste betrouwbaarheid en variantie oplevert (Eutsler & Lang, 2015; Kyriazos & Stalikas, 2018; Soto & John, 2019).

Gevoeligheid van de Cronbach’s alpha formule

De  bovenstaande formule laat zien dat de Cronbach’s alpha berekening gevoelig is voor extremen (outliers) in de dataset (Liu & Zumbo, 2007). Namelijk, als het verschil wordt berekend tussen een observatie en het gemiddelde, zal een extreme waarden tot een groot verschil leiden. Als daarna dit verschil ook nog wordt gekwadrateerd, zal deze extreme waarde een grote invloed hebben op de berekening. Dit probleem doet zich vooral voor als de extreme waarden aan een kant zitten, m.a.w. asymmetrisch zijn. De miswijzing ofwel bias kan volgens Liu and Zumbo (2007, p. 631) aanzienlijk zijn, een ware Cronbach’s alpha van 0.40 kan bijvoorbeeld door asymmetrische extreme waarden worden opgehoogd naar 0.80 tot 0.95. Daarentegen, als de ware Cronbach’s alpha (population reliability) al reeds hoog is, dan hebben asymmetrische extreme waarden geen noemenswaardig invloed. Het nadeel is, als je de Cronbach’s alpha meet zonder dat je de data inspecteert voor extreme waarden, is het onmogelijk om te bepalen of de hoge Cronbach’s alpha is veroorzaakt door extreme waarde of dat de ware Cronbach’s alpha wordt gemeten. Liu and Zumbo (2007) adviseren daarom ook om naast de Cronbach’s alpha meting een inspectie te doen op extreme waarden.

Hoe ziet de Cronbach’s alpha berekening er in tabel vorm uit?

Daarna tel je alle variantie van de vragen bij elkaar op.

Vervolgens moeten we de rij totalen bereken. Dit is de totale score van alle enquêtevragen per respondent. Hier tel je bijvoorbeeld alle antwoorden van respondent 1 bij elkaar op. En dit doe je daarna voor alle respondenten.

Daarna bepalen we de variantie van de rij-totalen.

Nu kunnen we het tweede deel van de Cronbach’s alpha formule voltooien. Het tweede deel resulteert in een waarde van 0.661473. Nu kunnen we de Cronbach’s alpha berekenen door het eerste en tweede deel met elkaar te vermenigvuldigen. Dit resulteert in Cronbach’s alpha van 1.25 * 0.661473 = 0.826841.

Wat houdt een negatieve Cronbach’s alpha in?

De Cronbach’s alpha test (Cronbach, 1951) wordt vaak gebruikt als indicator van interne consistentie (internal consistency). In sommige gevallen kan je een negatieve waarde krijgen van de Cronbach’s alpha. Een negatieve Cronbach’s alpha is volgens Krus and Helmstadter (1993) theoretisch en numeriek incorrect is, kan dit volgens Krus and Helmstadter (1993) en Helms, Henze, Sass, and Mifsud (2006) zijn veroorzaakt door een of meerdere omgekeerd gecodeerde schalen of als de items multidimensionaal zijn. Als de set van variabel multidimensionaal is, d.w.z dat zij niet 1 theoretisch construct meten, is misschien een andere samenstelling van de set met vragen noodzakelijk. Bij een negatieve Cronbach’s alpha is volgens Krus and Helmstadter (1993) een factor analyse noodzakelijk om duidelijkheid te verschaffen. In de factor analyse kan je namelijk controleren of alle item uni-dimensioneel zijn, maw dat ze maar 1 theoretisch construct meten.

Meet de Cronbach’s alpha de interne validiteit van je schalen?

Volgens (Helms et al., 2006) moet een onderzoeker er wel rekening mee houden dat interne consistentie niet het zelfde is als interne validiteit. De Cronbach’s alpha meet de interne consitentie, dus in hoeverre de items (vragen) die gebruikt zijn voor de berekening hetzelfde meten. Het zegt daarmee dus niet of de items meten wat de onderzoeker claimt wat de items meten.

Wanneer is de Cronbach’s alpha goed?

Nunnally (1967) geeft aan dat een Cronbach’s alpha van 0.50-0.60 gewenst is voor preliminairy research (early stages of research), voor basic research 0.80 en applied research 0.90-0.95 (Peterson, 1994). Maar, in een latere uitgave van zijn boek geeft Nunnally (1978) zonder onderbouwing aan dat een Cronbach’s alpha van 0.70 gewenst is voor preliminairy research, voor basic research 0.8 en applied research 0.90-0.95 (Nunnally & Bernstein, 1994; Peterson, 1994). Hierdoor citeren onderzoekers vaak wisselend tussen deze twee referenties. Als je in je enquête gevalideerde vragen hebt gebruikt, kan je je studie niet meer classificeren als preliminairy researchen zou je een hogere drempelwaarde voor je constructen moeten hanteren. Maar, let op, een Cronbachs alpha groter dan 0.90 wordt vaak gezien als een meeting met te veel redundanties.

De Cronbach’s alpha is gevoelig voor het aantal items

Pallant (2007, pp. 6-7) geeft aan dat de Cronbach’s alpha gevoelig is voor het aantal items (enquêtevragen) in de schaal. Cortina (1993, p. 102) en Schrepp (2020) versterken dit argument door aan te tonen dat als je 20 of meer items in je schaal hebt het vrij gemakkelijk is om een Cronbach’s alpha van 0.70 of meer te realiseren, zelfs als de items onderling maar beperkt gecorreleerd zijn. Pallant (2007) geven aan dat een schaal van minder dan 10 items een kleine Crombach’s alpha kan opleveren. Als je minder dan 10 items in je schaal hebt adviseert Pallant (2007, pp. 6-7) om gebruik te maken van de mean inter-item correlation. Een mean inter-item correlation tussen de 0.20 en 0.40 wordt als gewenst beschouwd (Briggs & Cheek, 1986). Briggs and Cheek (1986, p. 115) geven aan dat een mean inter-item correlation van minder dan 0.10 waarschijnlijk onvoldoende is om de complexiteit van het theoretisch construct in een variabele samen te vatten. Zij geven aan dat een mean inter-item correlation van meer dan 0.50 een indicatie is van redundante items in de schaal.

De Cronbach’s alpha is gevoelig voor het aantal observaties (respondenten)

De Cronbach’s alpha wordt berekend op basis van de onderlinge correlatie van de ingevoerde items (Likert-schaal vragen). Kortom, de Cronbach’s alpha bouwt voort op de aannames van een correlatieanalyse. Schönbrodt and Perugini (2013) hebben via een Monte-Carlo simulatie laten zien dat een correlatie analyse voor een laag aantal observaties onstabiel kan worden. Hiermee wordt bedoelt dat als een test herhaald wordt er een andere correlatie uitkomst uit komt. Zij adviseren, gebaseerd op de gewenste effect size (80%, 90% of 95%), dat de gewenste sample size 250 observaties is. Schrepp (2020) geeft aan dat er in een Cronbach’s alpha veel inter-correlaties zijn en is daardoor stabieler dan een enkele correlatie, maar het is duidelijk dat de grootte van de dataset een rol kan spelen in de hoogte van de Cronbach’s alpha. Daarom adviseert Schrepp (2020) om naast de Cronbach’s alpha ook zijn standaard error te vermelden, hiermee kan een lezer een inschatting doen van de betrouwbaarheid van de Cronbach’s alpha.

De berekening van de Cronbach’s alpha standaardfout en betrouwbaarheidsinterval

Uit het onderzoek van van Zyl, Neudecker, and Nel (2000)komt naar voren dat op basis van de aanname van multivariate normaliteit de standaard error van de Cronbach’s alpha versimpeld kan worden tot de formule vermeld in de artikelen van Duhachek, Coughlan, and Iacobucci (2005) en Forero (2014). Alleen is het wat lastig om de benodigde gegevens voor deze formule uit SPSS te halen.

De Cronbach’s alpha standaardfout en betrouwbaarheidsinterval in SPSS

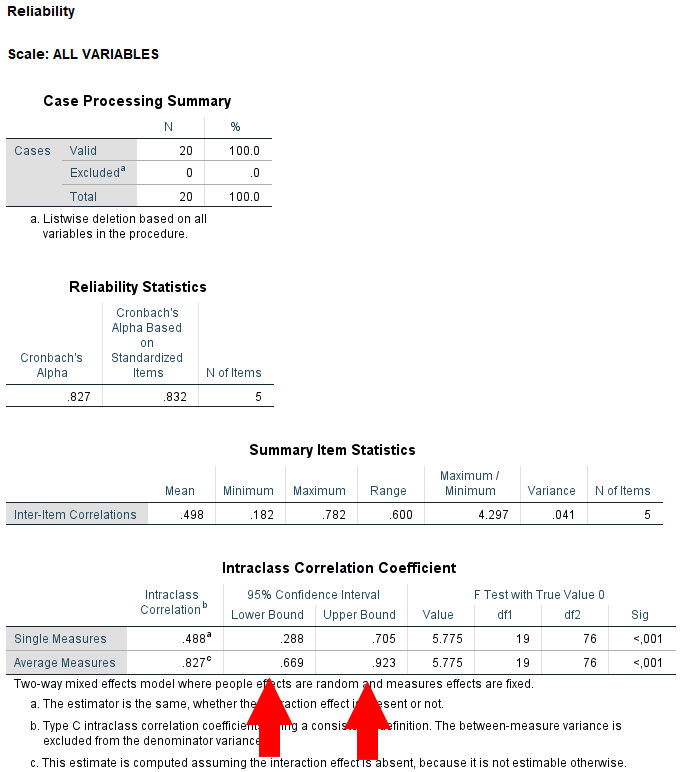
Een handigere optie om achter de standard error en 95% confidence interval van de Cronbach’s alpha te komen in terug te vinden in de FAQ’s van SPSS (IBM-SPSS-Statistics, 2020). In de FAQ’s van SPSS is terug te vinden dat als je via Anallyse=> Scale > Reliability Analysis de button Statistics aanklikt kan je de “Intraclass Correlation Coefficient” checkbox aanvinken. Als dan vervolgens bij “model” de “Two-Way Mixed” selecteert, kan je bij de ICC het confidence interval aflezen. Dit confindence interval is gelijk aan het confidence interval van de Cronbach’s alpha (Baumgartner & Chung, 2001; Bravo & Potvin, 1991). Wil je de standaard error weten, dan is het eenvoudig het gemiddelde van de upper confidence interval aftrekken, en daarna delen door 1.96.

Hoe bereken je het Cronbach’s alpha betrouwbaarheidsinterval in SPSS?

De mean item intercorrelation kan je berekenen in SPSS door eerst naar het menu van de Cronbach’s alpha te gaan. Selecteer Analyze => Scale => Reliability Analysis.

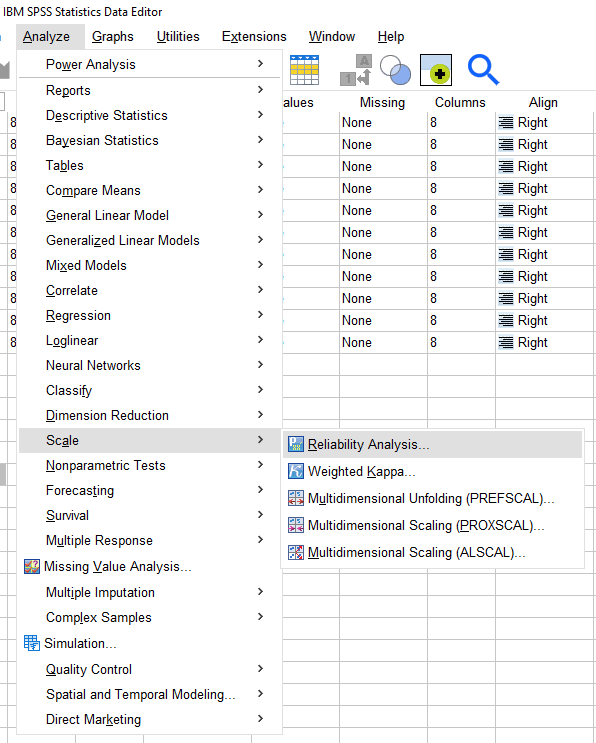
In het Cronbach’s alpha menu in SPSS selecteer je de intraclass correlation coefficient optie en selecteer je de two-way fixed optie.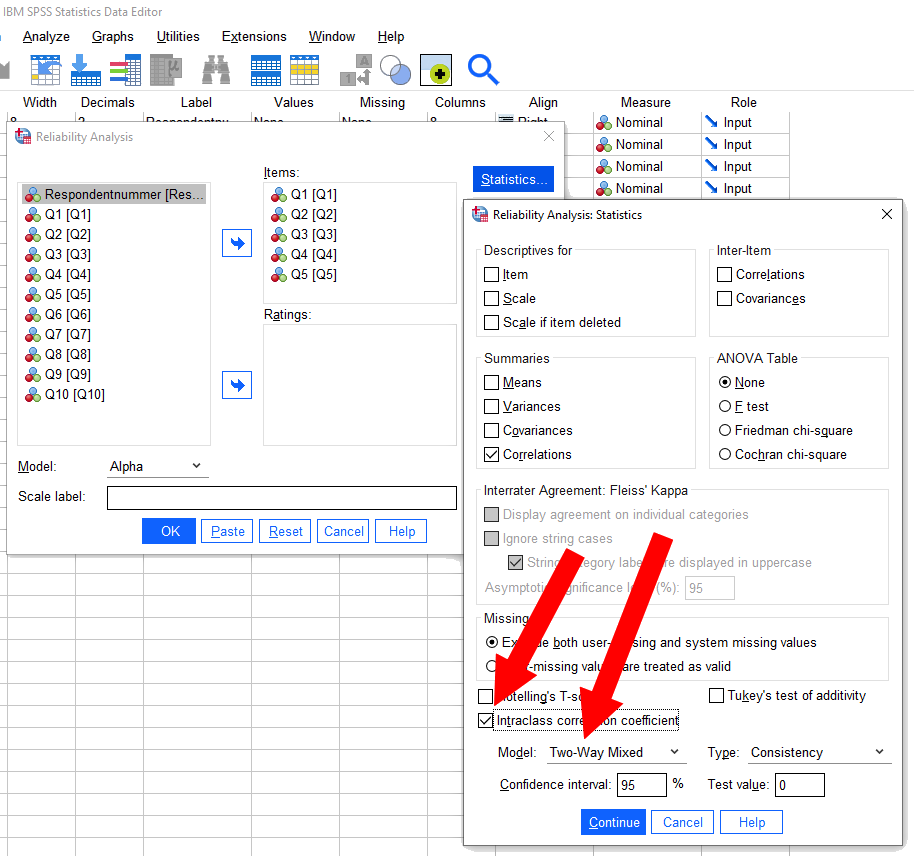

In het resultaten scherm (output) zie je dan onderaan bij de average meansures van de Intraclass Correlation Coefficient zie je het lower en upper confidence interval staan. Kortom, de tolerantie van de Cronbach’s alpha zit tussen deze grenzen.

De “rules of thumb” of bij de interpretatie van de Cronbach’s alpha

Naast de hiervoor vermelde drempelwaarden zijn er interpretatie tabellen voor de Cronbach’s alpha. Hieruit blijkt dat in de literatuur er geen consensus is over een absoluut minimum voor de Cronbach’s alpha. Bijvoorbeeld, de studie van Robertson and Evans (2020) en van Taber (2018) laten zien dat er een brede range is van kwalitatieve beschrijvingen van de Cronbach’s alpha. Denk er wel aan dat de meeste van deze schalen zijn gebaseerd op een schaal-lengte van ongeveer 20 vragen. Aangezien de Cronbach’s alpha gevoelig is voor het aantal vragen, is het verstandig dat dit meeneemt in je evaluatie. Hier zijn er twee kenmerkende publicaties die de onderzoekers een leidraad geven bij de interpretatie van de Cronbach’s alpha.

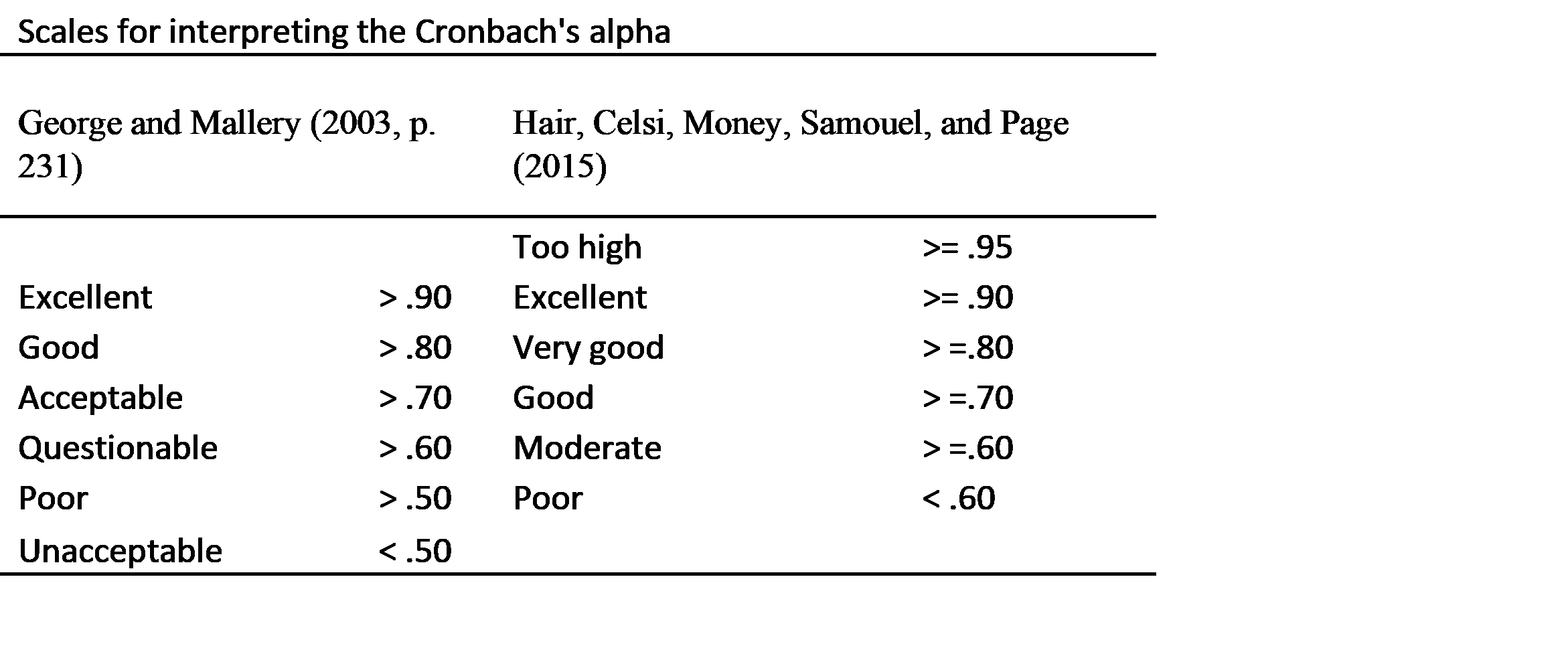
De Cronbach’s alpha is een indicatie van de meetfout (random variance)

De willekeurige variantie van een meervoudige meeting, m.a.w. meerdere Likert schaal items die een theoretisch construct meten, is een indicatie van de meetfout in een test. De meetfout kan bepaald worden met behulp van onderstaande formule.

Meetfout = 1 – α²

Bij een Cronbach’s alpha van:

• 0.60 is de meetfout dus 1 – (0.60 * 0.60) = 0.64.
• 0.70 is de meetfout dus 1 – (0.70 * 0.70) = 0.51.
• 0.80 is de meetfout dus 1 – (0.80 * 0.80) = 0.36.
• 0.90 is de meetfout dus 1 – (0.90 * 0.90) = 0.19.

Een grote Cronbach’s alpha bijvoorbeeld groter dan 0.90 hoeft niet per definitie te betekenen dat er veel interne consistentie is, en dus een kleine meetfout. Volgens Boyle (1991) kan dit ook betekenen dat er redundantie in de vragen zit, m.a.w. dat er met misschien iets andere bewoording, dezelfde vraag is gesteld.

De Cronbach’s alpha is gevoelig voor afwijkingen van normaalverdeling

De Cronbach’s alpha is volgens Wilcox (1992) en Spiliotopoulou (2009) gevoelig voor kleine afwijkingen van de normaal verdeling en gaat volgens Spiliotopoulou (2009) en Zimmerman, Zumbo, and Lalonde (1993) lineair aan elkaar verwant zijn. Als de variabelen hier niet aan voldoen onderschat de Cronbach’s alpha de interne consistentie van de variabelen.

De Cronbach’s alpha is gevoelig voor de schaallengte

Daarnaast heeft Cronbach (1951) al reeds geconstateerd dat zijn meting gevoelig is voor de schaallengte, m.a.w. het aantal liktert-schaal punten dat je gebruikt. Daarop heeft Cronbach (1951) een correctie formule bedacht om de alpha te corrigeren voor de schaallengte. Deze gecorrigeerde versie van de Cronbach’s alpha wordt in de literatuur vaak beschreven als de “average inter-item correlation”. De onderstaande formule is in lijn met de voorstellen van Cronbach (1951) en Voss, Stem, and Fotopoulos (2000).

α_corrected = α * 1 / (L + (L – 1)* α})

Waarbij:

α = De Cronbach’s alpha

L = Scale length, het aantal items in de schaal

De Cronbach’s alpha is gevoelig voor het aantal dimensies en mean item intercorrelation

Daarnaast heeft Cortina (1993) laten zien dat de Cronbach’s alpha afhankelijk is van de number of items, mean item intercorrelation en dimensionality. Cortina (1993) toon aan dat je een hoge Cronbach’s alpha kan hebben terwijl je een lage intercorrelatie tussen de items van je schaal hebt en/of dat er meer dan een dimensie wordt gemeten Cortina (1993). Met dit laatste wordt bedoeld dat je Cronbach’s alpha dus niet aantoont dat er maar een theoretisch construct wordt gemeten. Een schaal die unidimensioneel is heeft een hoge Cronbach’s alpha ongeacht hoeveel items er worden gebruikt Cortina (1993, p. 102). Dat is dus tegengesteld aan de intentie van je meting. Je gebruikt nu net de Cronbach’s alpha om aan te tonen dat er voldoende interne consistentie zit tussen je verschillende items (Likertschaal vragen), en dat je daarmee dus 1 onderliggend theoretisch construct meet. Daarom is het verstandig om naast de Cronbach’s alpha ook naar de mean item intercorrelation te kijken.

Mean item intercorrelation

De mean item intercorrelation is het gemiddelde tussen alle correlaties in je correlatie tabel. Clark and Watson (2016, p. 316) geven aan dat de individuele interitem correlaties tussen 0.15 en 0.50 zou moeten liggen. Waarbij een brede schaal, welke dus uit veel (Likert) vragen (items) bestaat een mean interitem correlatie tussen de 0.15 en 0.20 heeft. Een smalle schaal, welke uit weinig (Likert) vragen (items) bestaat een mean interitem correlatie tussen de 0.40 en 0.50 heeft. Maar zoals Cortina (1993) en (S. B. Green, Lissitz, & Mulaik, 1977) aangeeft, een hoge gemiddelde item intercorrelation is nog geen garantie dat je vragen maar 1 theoretisch construct meten. Je kan een hoge gemiddelde item intercorrelatie hebben maar toch een multidimensionele schaal hebben (Cortina, 1993). Daarom adviseren Clark and Watson (2016) en B. F. Green (1978) om te controleren of de interitem correlaties een gemiddelde sterkte hebben en dicht bij het gemiddelde liggen. MAW de interitem correlaties moeten een lage spreiding hebben.

Mean item intercorrelation in SPSS

De mean item intercorrelation kan je berekenen in SPSS door eerst naar het menu van de Cronbach’s alpha te gaan. Selecteer Analyze => Scale => Reliability Analysis.

In het Cronbach’s alpha menu in SPSS selecteer Correlations in het Summaries menu.

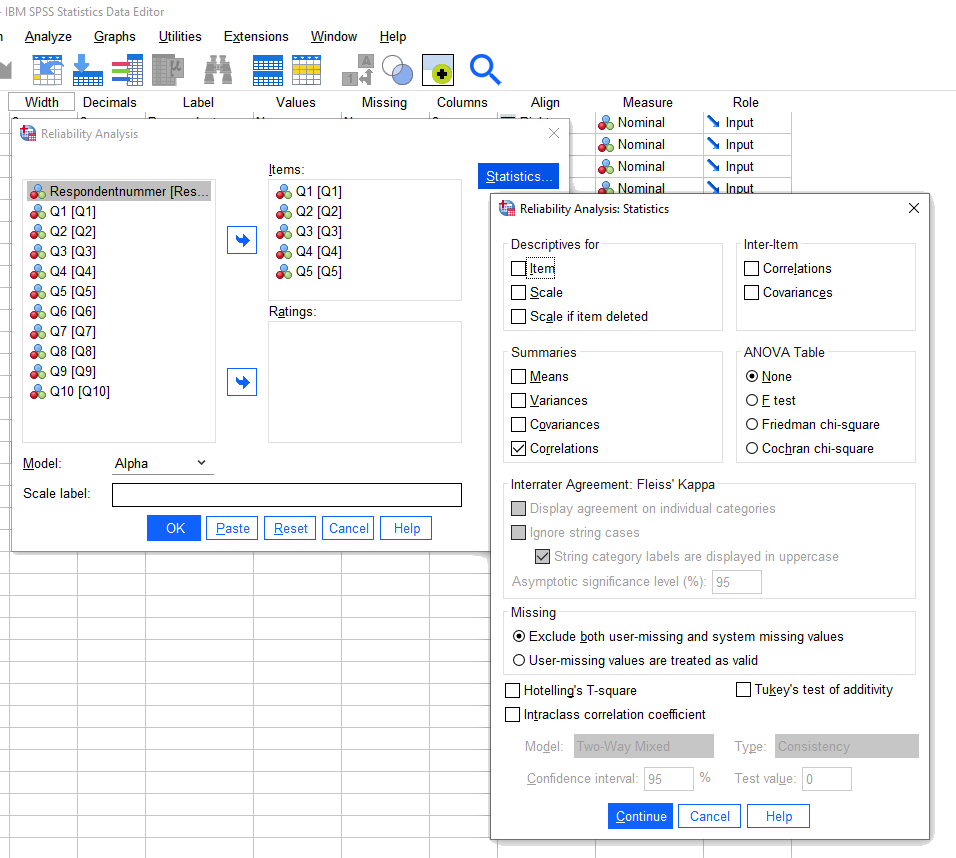
In de results window zie je onderaan de mean inter-item correlation staan.

Wat als de Cronbach’s alpha lager is dan 0.70?

De praktische toepassing van voorgaande adviezen is te vinden in het artikel van Moynihan and Schuitema (2020, pp. 6-7). Moynihan and Schuitema (2020, pp. 6-7) argumenteren dat hun conservatism scale niet voldoet aan de richtlijnen van Nunnally (1978) met betrekking tot een Cronbach’s alpha van minimal 0,70. Zij argumenten dat korte schalen, met minder dan 10 items (vragen) het heel normaal is dat de Cronbach’s alpha lager is dan 0,70. Daarom gebruiken zij op advies van Briggs and Cheek (1986) de interitem correlatie in plaats van de Cronbach’s alpha. Zij geven aan dat de optimale range voor de interitem correlatie tussen de 0.20 en 0.40 ligt (Briggs & Cheek, 1986, p. 115).

Een andere praktische toepassing is de vinden in het artikel van Razmerita, Kirchner, Hockerts, and Tan (2020, p. 483). Net als Moynihan and Schuitema (2020, pp. 6-7) geven zij aan dat de Cronbach’s alpha berekend op minder dan 10 items laag is en dat op basis van het advies van Briggs and Cheek (1986) om de interitem correlatie te gebruiken. Zij gebruiken ook de richtlijn dat de optimale range voor de interitem correlatie tussen de 0.20 en 0.40 ligt (Briggs & Cheek, 1986, p. 115).

Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.

Contact! >>     WhatsApp Ons! >>

Ben je benieuwd wat onze scriptiebegeleiding (scriptiehulp) je kost? Neem dan een kijkje op onze tarievenpagina via onderstaande button!

Wat kost scriptiebegeleiding? >>

Literatuurlijst:

1. Baumgartner, T. A., & Chung, H. (2001). Confidence Limits for Intraclass Reliability Coefficients. Measurement in Physical Education and Exercise Science, 5(3), 179-188. doi:10.1207/S15327841MPEE0503_4
2. Boyle, G. J. (1991). Does item homogeneity indicate internal consistency or item redundancy in psychometric scales? Personality and Individual Differences, 12(3), 291-294. doi:10.1016/0191-8869(91)90115-R
3. Bravo, G., & Potvin, L. (1991). Estimating the reliability of continuous measures with cronbach’s alpha or the intraclass correlation coefficient: Toward the integration of two traditions. Journal of Clinical Epidemiology, 44(4), 381-390. doi:10.1016/0895-4356(91)90076-L
4. Briggs, S. R., & Cheek, J. M. (1986). The role of factor analysis in the development and evaluation of personality scales. Journal of Personality, 54(1), 106-148. doi:10.1111/j.1467-6494.1986.tb00391.x
5. Clark, L. A., & Watson, D. (2016). Constructing validity: Basic issues in objective scale development. Washington, DC, US: American Psychological Association.
6. Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications. Journal of Applied Psychology, 78(1), 98-104. doi:10.1037/0021-9010.78.1.98
7. Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16(3), 297-334. doi:10.1007/bf02310555
8. Duhachek, A., Coughlan, A. T., & Iacobucci, D. (2005). Results on the Standard Error of the Coefficient Alpha Index of Reliability. Marketing Science, 24(2), 294-301. doi:10.1287/mksc.1040.0097
9. Eutsler, J., & Lang, B. (2015). Rating Scales in Accounting Research: The Impact of Scale Points and Labels. Behavioral Research in Accounting, 27(2), 35-51. doi:10.2308/bria-51219
10. Forero, C. G. (2014). Cronbach’s Alpha. In A. C. Michalos (Ed.), Encyclopedia of Quality of Life and Well-Being Research (pp. 1357-1359). Dordrecht: Springer Netherlands.
11. George, D., & Mallery, P. (2003). SPSS for Windows Step by Step: A Simple Guide and Reference, 11.0. In. Boston, Massachusetts: Allyn and Bacon.
12. Green, B. F. (1978). In defense of measurement. American Psychologist, 33(7), 664-670. doi:10.1037/0003-066X.33.7.664
13. Green, S. B., Lissitz, R. W., & Mulaik, S. A. (1977). Limitations of Coefficient Alpha as an Index of Test Unidimensionality. Educational and Psychological Measurement, 37(4), 827-838. doi:10.1177/001316447703700403
14. Hair, J. F., Celsi, M., Money, A., Samouel, P., & Page, M. (2015). The Essentials of Business Research Methods. In (3 ed.). New York, NY: Routledge.
15. Helms, J. E., Henze, K. T., Sass, T. L., & Mifsud, V. A. (2006). Treating Cronbach’s Alpha Reliability Coefficients as Data in Counseling Research. The Counseling Psychologist, 34(5), 630-660. doi:10.1177/0011000006288308
16. IBM-SPSS-Statistics. (2020). Confidence interval for Cronbach’s alpha in SPSS. Retrieved from https://www.ibm.com/support/pages/confidence-interval-cronbachs-alpha-spss
17. Krus, D. J., & Helmstadter, G. C. (1993). The Problem of Negative Reliabilities. Educational and Psychological Measurement, 53(3), 643-650. doi:10.1177/0013164493053003005
18. Kyriazos, T. A., & Stalikas, A. (2018). Applied Psychometrics: The Steps of Scale Development and Standardization Process. Psychology, 9(11), 2531-2560. doi:10.4236/psych.2018.911145
19. Liu, Y., & Zumbo, B. D. (2007). The Impact of Outliers on Cronbach’s Coefficient Alpha Estimate of Reliability: Visual Analogue Scales. Educational and Psychological Measurement, 67(4), 620-634. doi:10.1177/0013164406296976
20. Moynihan, A. B., & Schuitema, G. (2020). Values Influence Public Acceptability of Geoengineering Technologies Via Self-Identities. Sustainability, 12(11), 4591. doi:10.3390/su12114591
21. Nunnally, J. C. (1967). Psychometric theory. New York: McGraw-Hill.
22. Nunnally, J. C. (1978). Psychometric Theory. New York, NY, USA: McGraw-Hill.
23. Nunnally, J. C., & Bernstein, I. H. (1994). Psychometric theory (3 ed.). New York: McGraw-Hill.
24. Pallant, J. (2007). SPSS survaival manual: A step by step guide to data analysis using SPSS for Windows (Version 10). Ballmoor, Buckingham: Open University Press.
25. Peterson, R. A. (1994). A Meta-analysis of Cronbach’s Coefficient Alpha. Journal of Consumer Research, 21(2), 381-391. doi:10.1086/209405
26. Razmerita, L., Kirchner, K., Hockerts, K., & Tan, C.-W. (2020). Modeling Collaborative Intentions and Behavior in Digital Environments: The Case of a Massive Open Online Course (MOOC). Academy of Management Learning & Education, 19(4), 469-502. doi:10.5465/amle.2018.0056
27. Robertson, O., & Evans, M. S. (2020). Just how reliable is your internal reliability? An overview of Cronbach’s alpha (α). Retrieved from Leicester, UK:
28. Schönbrodt, F. D., & Perugini, M. (2013). At what sample size do correlations stabilize? Journal of Research in Personality, 47(5), 609-612. doi:10.1016/j.jrp.2013.05.009
29. Schrepp, M. (2020). On the Usage of Cronbach’s Alpha to Measure Reliability of UX Scales. Journal of Usability Studies, 15(4), 247-258.
30. Soto, C. J., & John, O. P. (2019). Optimizing the length, width, and balance of a personality scale: How do internal characteristics affect external validity? Psychological Assessment, 31(4), 444-459. doi:10.1037/pas0000586
31. Spiliotopoulou, G. (2009). Reliability reconsidered: Cronbach’s alpha and paediatric assessment in occupational therapy. Australian Occupational Therapy Journal, 56(3), 150-155. doi:10.1111/j.1440-1630.2009.00785.x
32. Taber, K. S. (2018). The Use of Cronbach’s Alpha When Developing and Reporting Research Instruments in Science Education. Research in Science Education, 48(6), 1273-1296. doi:10.1007/s11165-016-9602-2
33. van Zyl, J. M., Neudecker, H., & Nel, D. G. (2000). On the distribution of the maximum likelihood estimator of Cronbach’s alpha. Psychometrika, 65(3), 271-280. doi:10.1007/BF02296146
34. Voss, K. E., Stem, D. E., & Fotopoulos, S. (2000). A Comment on the Relationship between Coefficient Alpha and Scale Characteristics. Marketing Letters, 11(2), 177-191. doi:10.1023/A:1008146924781
35. Wilcox, R. R. (1992). Robust generalizations of classical test reliability and Cronbach’s alpha. British Journal of Mathematical and Statistical Psychology, 45(2), 239-254. doi:10.1111/j.2044-8317.1992.tb00990.x
36. Zimmerman, D. W., Zumbo, B. D., & Lalonde, C. (1993). Coefficient Alpha as an Estimate of Test Reliability Under Violation of Two Assumptions. Educational and Psychological Measurement, 53(1), 33-49. doi:10.1177/0013164493053001003

Geïnteresseerd in onze andere Tips? >>