Wat is de ideale onafhankelijke variabele in een OLS-regressie?

De ideale onafhankelijke variabele is een variabele die “zuiver” gemeten is. Dat wil zeggen dat deze variabele (X1) uitsluitend en alleen een eigenschap meet en geen overlap (correlatie) heeft met een andere variabele (X2) in het model (Thompson, 2006, pp. 232-234). Er wordt ook wel gezegd dat X1 en X2 dan orthogonaal zijn Kennedy (2002).  In dit geval zijn de beta gewichten gelijk aan de correlatiecoëfficiënten (Thompson, 2006, pp. 232-234). Wat eenvoudiger geformuleerd, als er geen overlap tussen de variabelen is, is de gestandaardiseerde beta (β) van de regressie gelijk aan de rho (r) van je correlatieanalyse (Thompson, 2006, pp. 232-234). En is de som van de gekwadrateerde structure coefficients gelijk aan je R-squared (Courville et al., 2001; Thompson, 2006, pp. 232-234).

Visualisatie van regressieanalyses door middel van Ballantine’s

Een veel gebruikte visualisatietechniek van regressieanalyses is een Venndiagram (Kennedy, 2002). Deze Venndiagrammen zijn voor het eerst gebruikt door Cohen et al. (1975) en zij noemden dit “Ballantine”. Kennedy (1981) heeft het gebruik van Ballantine’s verder uitgebreid om hiermee ook bias en variance te visualiseren. Ip (2001) heeft voorgaand onderzoek uitgebreid met de visualisatie van suppressor variabelen doormiddel van Ballantine’s. Een eenvoudige uitleg van het gebruik van Ballantine’s is te vinden in het artikel van O’Brien (2018) , Kennedy (2002) en Ip (2001).

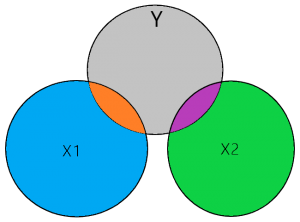
De ideale situatie

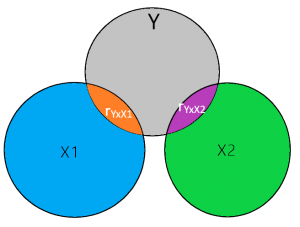
In de figuur hierboven illustreert het grijze gebied de variatie in de variabele Y, het blauwe gebied illustreert de variatie in variabel X1, en het groene gebied illustreert de variatie in variabele X2. Als je een idee wil hebben hoe groot de cirkel van het venndiagram is zou je als indicatie in je beschrijvende data kunnen kijken naar de variantie of een afgeleide daarvan de standaarddeviatie. De standaarddeviatie is de wortel van de variatie. Hierbij gaan we er voor deze uitleg wel vanuit dat je interval of ratio (continue) variabelen gebruikt die normaal zijn verdeeld.

Gratis Intakegesprek? >>

Het bepalen van de Bèta coëfficiënten

De bèta van een OLS-regressie kan wordt berekend door de covariantie tussen de X variabele en de Y variabele te delen door de variantie van de X variabele. Met andere woorden als de X variabele 1 eenheid verandert, hoeveel verandert dan de gemeenschappelijke variantie tussen X en Y. De bèta coëfficiënt van je regressie is in wezen de hellingshoek tussen de verandering van je X variabele EN de gemeenschappelijke verandering X en Y variabele.

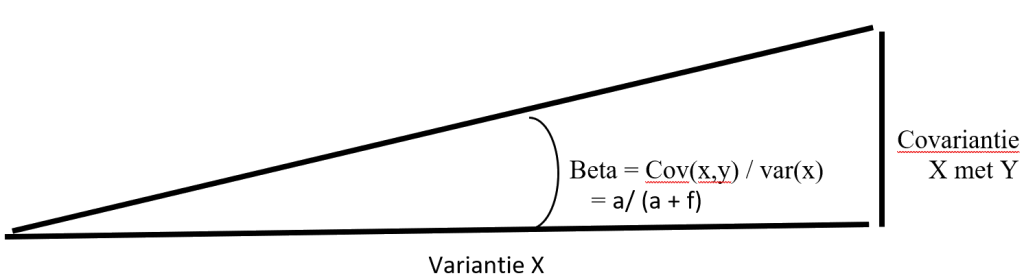
Wat is een variantie?

De variantie van een X observatie is het verschil tussen een observatie en de gemiddelde waarde van alle observaties in het kwadraat (X – X gemiddeld)². Hier nemen we het gekwadrateerde verschil omdat anders observaties lager dan het gemiddelde observaties hoger dan het gemiddelde zouden kunnen compenseren. Door het kwadraat te nemen kijken we min of meer naar de absolute waarde van het verschil. Om van een observatie naar een uitspraak over alle observaties te komen nemen we het gemiddelde van alle gekwadrateerde verschillen

Wat is een covariantie?

De covariantie is hier een eenvoudige uitbreiding op. De covariantie is in essentie de vermenigvuldiging tussen de variantie van de Y variabele en de variantie van de X variabele.

Hoe kan je de Bèta coëfficiënten visualiseren in een Ballantine?

Het oranje gebied (a) vormt hier de gemeenschappelijke variatie (covariantie) van X1 en Y. Het paarse gebied (b) vormt hier de gemeenschappelijke variatie (covariantie) van X2 en Y. De combinatie van het oranje (a) en het paarse gebied (b) stelt de R-squared van de regressie voor, m.a.w. het percentage van de verandering in Y dat door de som van correlatie tussen Y en X1 en Y en X2 worden verklaard.

Het grijze gebied (e) is het gebied van Y dat NIET door het oranje (a) en paarse (b) gebied wordt verklaard. Het grijze gebied ( e) gebied kan je in de ballantine beschouwen als de error term in je regressie (Kennedy, 2002).

In deze situatie zou je de R-squared van je model gelijk kunnen stellen aan de som van de gekwadrateerde structure coefficients (Courville et al., 2001; Thompson, 2006, pp. 232-234).

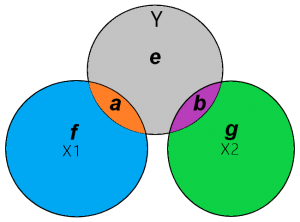
De bèta van je regressietabel zou je kunnen bereken met onderstaande formule.

De regressie coëfficiënt ofwel de hellingshoek (O’Brien, 2018):

• β₁ = a / (a + f)
• β₂ = b / (b + g)

Als je een Pearson correlatie tabel hebt van je variabelen, dan zou je de bèta coëfficiënten als volgt kunnen uitrekenen (Thompson, 2006, pp. 232-234):

• β₁ =  r_y*x1
• β₂ = r_y*x2

In bovenstaand voorbeeld gaan we, even extreem gesteld, er van uit dat als je naar je correlatie tabel kijkt dat alle onafhankelijke (inclusief controle variabelen) een correlatie hebben met je afhankelijke variabele maar niet met elkaar. Je kan je voorstellen dat dit een theoretische situatie is die zo nu en dan ook in de praktijk voorkomt, maar je verwacht eerder dat de onafhankelijke variabelen onderling gecorreleerd zijn. Daarom bespreken we op de volgende pagina een meer praktische situatie.

Geïnteresseerd in onze andere Tips? >>

Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.

Contact! >>     WhatsApp Ons! >>

Literatuurlijst:

1. Cohen, J., & Cohen, P. (1975). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. Hillside, NJ: Lawrence Erlbaum Associates.
2. Courville, T., & Thompson, B. (2001). Use of Structure Coefficients in Published Multiple Regression Articles: β is not Enough. Educational and Psychological Measurement, 61(2), 229-248. 
3. Lp, E. H. S. (2001). Visualizing multiple regression. Journal of Statistics Education, 9(1)
4. Kennedy, P. E. (1981). The “ballentine”: A graphical aid for econometrics*. Australian Economic Papers, 20(37), 414-416. 
5. Kennedy, P. E. (2002). More on venn diagrams for regression. Journal of Statistics Education, 10(1), 1-10. 
6. O’Brien, R. M. (2018). A consistent and general modified Venn diagram approach that provides insights into regression analysis. PLOS ONE, 13(5), 1-12. 
7. Thompson, B. (2006). Foundations of Behavioral Statistics: An Insight-Based Approach. New York: Guilford Publications.