Omitted Variable Bias vanuit een Ballentine perspectief
Als we de Omitted Variable Bias (OVB) bekijken vanuit een Ballentine perspectief dan bekijken we eerst de verwachte situatie. Laten we het aantal medewerkers voorbeeld er weer bij nemen.
Stel we willen in onze scriptie het effect van de grootte van de organisatie op de omzet meten. Dit lijkt een inkoppertje, een grotere organisatie heeft meer omzet. Maar, zoals we al eerder hebben besproken, het aantal medewerkers meet niet alleen en uitsluitend de grootte van de organisatie. Stel, dat we naast het aantal medewerkers ook nog een variabele opnemen die de industriesector meet. Dan wordt de relatie tussen het aantal medewerkers en de omzet gecorrigeerd voor de industriesector waar de organisatie in zit.
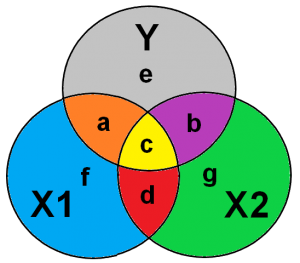
Figuur 1
Wat veroorzaakt Omitted Variable Bias?
Nu komt de twist in dit verhaal. In de praktijk zijn we niet altijd op de hoogte van alle relevante beïnvloedende variabelen van onze afhankelijke variabele. Daarnaast, zelfs als we weten dat een bepaalde variabele relevant is, hebben we niet altijd data van deze variabele. Dus, er is een realistische kans dat je relevante variabele vergeet mee te nemen in je regressiemodel. Dan spreken we dus van een OVB.
Waarom is Omitted Variable Bias nu een probleem?
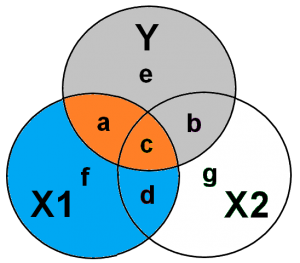
Figuur 2
Stel, dat in ons voorbeeld we variabele X2 vergeten mee te nemen (Figuur 2). X2 is in figuur 2 dan de industriesector van een organisatie. Het weglaten van X2 zorgt ervoor dat de variatie welke niet uniek was voor X1 (gebied c (geel) in figuur 2) weer bij gebied a wordt opgeteld. Kortom, variabele X1 krijgt nu onterecht gemeenschappelijke variatie met variabele Y toegewezen. Dit veroorzaakt een “bias” in variabele X1. Naast deze “bias” zorgt de toename van het oranje gebied (a + c) dat er meer informatie wordt meegenomen. Hierdoor neemt de variantie af, omdat de variantie gelijk is aan het gemiddelde van de gekwadrateerde verschillen t.o.v. het gemiddelde. Doordat er meer waarden worden meegenomen wordt de invloed van extreme waarden minder. Hierdoor wordt je regressiecoëfficiënt nauwkeuriger.
Het nadelige effect van Omitted Variable Bias
Daarnaast wordt de error-term vergroot omdat in figuur 2 gebied b (paars) bij gebied e (grijs) wordt opgeteld. Deze vergrootte error-term kan ertoe leiden dan de standaard error, 95% betrouwbaarheidsinterval, en de p-waarde van je regressiecoëfficiënt worden vergroot. Hiermee wordt de “bias” in de schatting van je regressiecoëfficiënt weer verhoogd. Aangezien de t-waarde van je regressiecoëfficiënt wordt bepaald door de wortel van de ratio van √ (a + c ) / ((e + b) * (n-k-1)). Is de verandering in de t-waarde afhankelijke van de verhouding tussen het gele gebied c en het paarse gebied b.
Samenvattend
Kortom, in het geval van OVB kan de significantie, sterkte en teken van je regressiecoëfficiënt beter of slechter worden afhankelijk van de verhouding tussen het gele gebied c en het paarse gebied b. In een regressieanalyse is ons doel om een verklarend of voorspellend model te maken van een causale relatie. We willen daarbij een bias minimaliseren want een bias zorgt voor dat je regressiecoëfficiënt qua sterkte en qua teken afwijkt. Daarom blijft het doel om relevante verklarende variabelen op te nemen in het model. Wanneer weet je nou dat je genoeg verklarende variabelen hebt en je bias dus er niet of beperkt is?
Hoe kan je testen voor Omitted Variable Bias?
Er zijn verschillende manieren waarop je kan controleren voor OVB. In Stata kan je na je regressie het commando rvfplot gebruiken. De scatterplot welke je dan krijgt tussen de voorspelde waarden en de residuen vergelijken met de voorbeelden van Condor dePaul. Daarnaast kan je in Stata de Ramsey RESET test gebruiken. Als de Ramsey RESET test significant is kan je er van uit gaan dat je OVB hebt. In SPSS kan je bij de plots een plot tussen de residuals en de predicted values opvragen voor een visuele inspectie. De scatterplot welke je dan krijgt tussen de voorspelde waarden en de residuen vergelijken met de voorbeelden van Condor dePaul. Daarnaast kan je in SPSS ook een Ramsey RESET test doen, alleen vraagt deze test in SPSS wat meer handelingen.
Geïnteresseerd in onze andere Tips? >>
Hoe kan je Omitted Variable Bias oplossen?
Two-stage least-squares regression (2SLS)
Als je ondanks het toevoegen van relevante variabelen nog steeds bias in je OLS-regressie houdt zijn er twee alternatieven. Je kan overstappen op een instrumental variable regression zoals een two-stage least-squares regression (2SLS) (Becker, 2016). Het nadeel van een 2SLS is dat je instrumentele variabele nodig hebt. Als het instrument te zwak is kan het de bias vergroten i.p.v. verkleinen. Het vinden van de juiste instrumentele variabelen is een complex proces. Dit komt omdat je instrument exogeen moet zijn. Dit wil zeggen dat het gecorreleerd is met je endogene onafhankelijke variabele maar niet met de error-term van je afhankelijke variabele. Een interessante methode om in je scriptieonderzoek een instrumentele variabele te creëren is door middel van het bepalen van een industrie gemiddelde waarbij de focal firm wordt uitgesloten (Germann, Ebbes, & Grewal, 2015). In Stata kan je de kwaliteit van je instrumental variable testen met het ivreg2 commando.
Fixed Effects regressie (FE)
Je kan overstappen op een fixed-effects (FE) regression model indien de OVB time-invariant is. In een FE-regression wordt er gecontroleerd voor de OVB door de manier waarop de regressiecoëfficiënt wordt berekend. Het nadeel van een FE-regressie is wel dat je hier panel-data voor nodig hebt. In panel-data heb je een herhaalde meting van hetzelfde object. Bijvoorbeeld, je kijkt naar de jaarlijkse omzet van de bedrijven over een periode van 5 jaar. Een FE is tevens een regressietechniek welke kijkt naar de verandering van je variabele in de tijd. Dus, variabelen die niet veranderen in de tijd worden verwijderd uit de analyse. Een FE-regressie is daarom minder geschikt als je meerdere industrieën of landen gebruikt. Want de firm fixed effects variabelen veranderen niet in de tijd en worden daarom in de FE-regressie verwijderd. Als de OVB verandert in de tijd dan is een First Difference regressiemodel meer van toepassing (Amartey, 2020).
Tot slot
Kortom, zowel een instrumental variable regression als een fixed effects regression hebben hun beperkingen. Daarom is het verstandig om op basis van de literatuur alle relevante controle variabelen mee te nemen. Alleen als voorgaande niet werkt is het verstandig om naar een instrumental variable regression of een fixed effects regression over te stappen.
Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.
Literatuurlijst:
- Amartey, P. (2020). A comparison of some estimation methods for handling omitted variables : a simulation study.
- Becker, S. O. (2016). Using instrumental variables to establish causality. IZA World of Labor, 250.
- Germann, F., Ebbes, P., & Grewal, R. (2015). The Chief Marketing Officer Matters! Journal of Marketing, 79(3), 1-22.