Hoeveel variabelen kan mijn dataset aan?
Hoeveel variabelen je in een meervoudige (multipele) lineaire regressie kan opnemen is van een aantal factoren afhankelijk. Je hebt waarschijnlijk wel eens gelezen dat er vuistregels zijn voor hoeveel observaties je nodig hebt bij een X aantal regressievariabelen. Een zeer bekende vuistregel is geschreven door Tabachnick and Fidell (2007, pp. 123-124). Zij stellen dat het minimale aantal observaties gelijk is aan 50 plus 8 x het aantal regressie variabelen. Hierbij gaan zij er van uit dat α =0.05, β = 0.20 (power is 80%) en een medium effect size (f2 = 0.15). Dit is een vrij grove benadering (over het waarom komen we aan het einde van deze pagina terug). Daarom lichten we hieronder een, volgens ons, betere methode toe op basis van het programma G*Power. G*Power is een veelzijdig statistisch programma dat gratis ter beschikking wordt gesteld door de Die Heinrich-Heine-Universität Düsseldorf.
Het voordeel van werken met G*Power is dat je een veel verfijndere methode kan toepassen. G*Power helpt je om het verband tussen steekproefomvang (sample size), de kleinste verschillen die je wil detecteren (effect size), de kans op een type I fout (α) en de kans op een type II fout (β) zichtbaar te maken. Je kan met dit programma in beeld brengen hoe deze vier factoren elkaar beïnvloeden.
Hieronder lichten we eerst even deze vier factoren toe.
Wat is de steekproefomvang?
Dit is de grootte van de groep observaties/enquêteresultaten/respondenten waarvan je voor alle variabelen een goed waarde hebt. Hierbij gaan we er van uit dat de SPSS/ Stata dataset gecontroleerd is op missende, foutief of onwaarschijnlijke grote of kleine waarden. Met andere woorden, het eerste en belangrijkste proces is om de “vervuiling” uit de data te halen. Aangezien dit proces je selectie-bias kan verhogen, is het belangrijk om te motiveren en onderbouwen waarom desbetreffende observaties zijn verwijderd. De dataset die je na het opschonen overhoudt is je steekproefomvang.
Wat is een effect size?
Een effect size in zijn eenvoudigste vorm is het verschil tussen twee populatie gemiddelden. Stel dat vrouwen gemiddeld genomen € 30.000 per jaar verdienen en mannen € 40.000 per jaar, dan is de effect size € 40.000 – € 30.000 = € 10.000. Deze € 10.000 is informatief, maar is afhankelijk van de schaal waarop is gemeten. Daarnaast geeft deze € 10.000 niet aan of dit een klein of groot verschil is t.o.v. de twee populatie gemiddelden. Hier mist namelijk een referentieniveau. Als we er van uit gaan dat de spreiding rondom het gemiddelde salaris van vrouwen en mannen gelijk is, dan kunnen deze € 10.000 delen door de standaarddeviatie van de groep vrouwen of mannen. In dit voorbeeld nemen we aan dat de standaarddeviatie €15.000 is. Dan is de Cohens effect size gelijk aan (€40.000 – €30.000)/ €15.000 = 0,67.
Als je meer uitleg van een effect size zoekt klik dan op deze link.
Wat betekend de kans op een type I fout (α)?
De alpha (α) is ook bekend onder de Type I foutkans. Een Type I fout kan worden beschouwd als een situatie waarin je een ongeldig alternatieve hypothese (HA) als waar aanneemt. Daarmee verwerp je dus onterecht de nulhypothese (H0). Bijvoorbeeld, je claimt dat een bepaald medicijn patiënten geneest, terwijl in werkelijkheid de patiënten er juist zieker van worden. Hierbij stellen we dus als nulhypothese dat het medicijn de patiënten niet geneest. Het doel van de test is dan ook om de nulhypothese te verwerpen. Het gevaar van een Typ I error is dat als je denkt dat een medicijn werkt, je het niet opnieuw gaat testen. Immers, je gaat er van uit dat de werking is bewezen. In de sociale wetenschappen hebben we een conventie dat een Type I foutkans van minder dan 1 op 20 acceptabel is. Kortom, een α van minder dan 0.05 wordt als acceptabel beschouwd.
Wat betekend de kans op een type II fout (β)?
De bèta (β) is ook bekend onder de Type II foutkans. Een Type II fout kan worden beschouwd als een situatie waarin je een ongeldige nulhypothese (H0) als waar aanneemt. Daarmee verwerp je dus onterecht de alternatieve hypothese (HA). Als we weer naar het medicijn voorbeeld kijken, dan claim je dus dat een bepaald medicijn niet werkt, terwijl in werkelijkheid patiënten wel baadt hebben van het medicijn. Een Type II fout is minder schadelijk dan een Type I fout omdat, als je ervan overtuigd bent dat een medicijn werkt, je het ongetwijfeld gaat her-testen en ontdek je je eerdere fout. Statistisch power (1-β), is de kans (detectievermogen) dat je een effect in je data vindt, op de voorwaarde dat het effect ook daadwerkelijk in je data zit. In statistische power analyse worden doorgaans de drempelwaarden van 80%, 90%, of 95% gebruikt.
In onderstaande tabel hebben we de type I foutkans, type II foutkans, power en betrouwbaarheidsinterval in een matrix uitgezet.

Hoe kan je het samenspel van je type I fout, type II fout, steekproefomvang, effect size en aantal variabelen voorstellen?
In onderstaande figuur hebben we de type I foutkans, type II foutkans, effect size en steekproefomvang grafisch weergegeven. In deze figuur hebben we een extra element toegevoegd, dat is wat het effect is van het aantal regressievariabelen wat je wil gebruiken. Stel je eens voor dat je net genoeg observaties hebt verzameld om voor drie regressievariabelen een gemiddelde effect size (f2 =0.15) een significantie van 5% en een power (1- β) van 80% te meten. Als je dan meer controle variabelen wil toevoegen zullen de pijlen naar buiten worden gedrukt. Je kan tot drie van de vier pijlen constant houden maar de vierde zal het grotere aantal variabelen moeten compenseren. Als je bijvoorbeeld niet in staat bent om meer observaties te verzamelen en geen concessies wil doen aan de type I foutkans, type II foutkans, dan moet je accepteren dat je alleen grotere effecten kan detecteren.
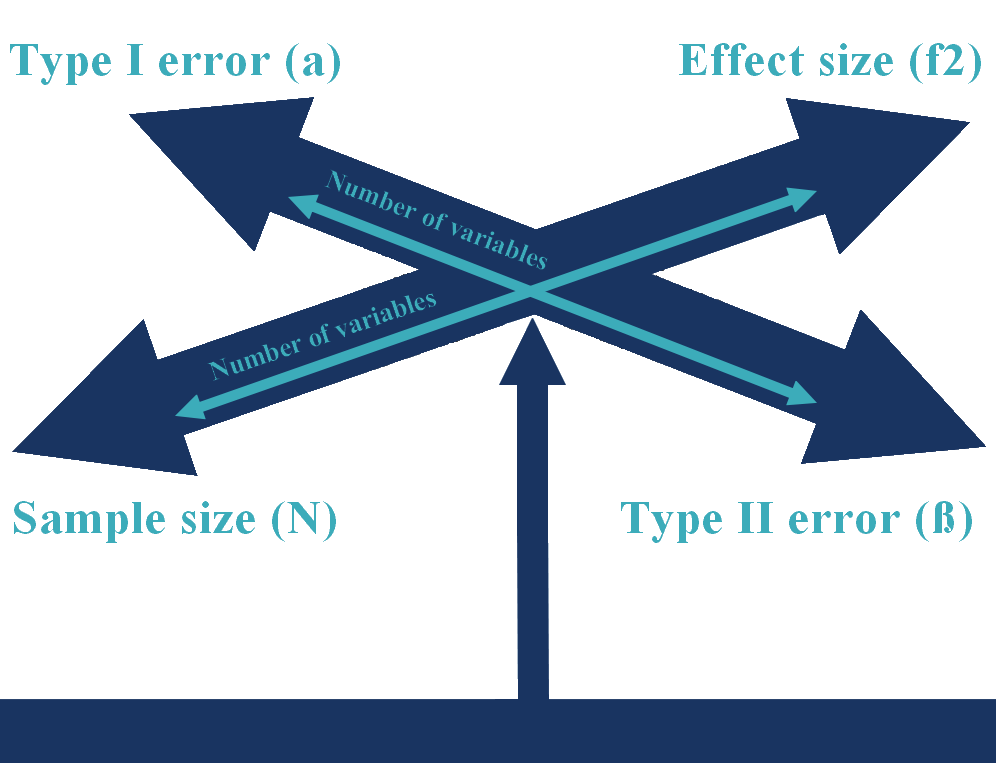
Het aantal regressievariabelen op basis van G*Power.
G*Power helpt ons om vast te stellen hoeveel variabelen onze SPSS/ Stata dataset aan kan. In dit eerste voorbeeld gaan we er van uit dat je werkt met een standaard OLS-regressie, normaal verdeelde variabelen en geen hiërarchisch model hebt. We laten met behulp van screenschots stap voor stap zien hoe je de analyse kan doen.
Stap 1:
Het beginscherm van G*Power.
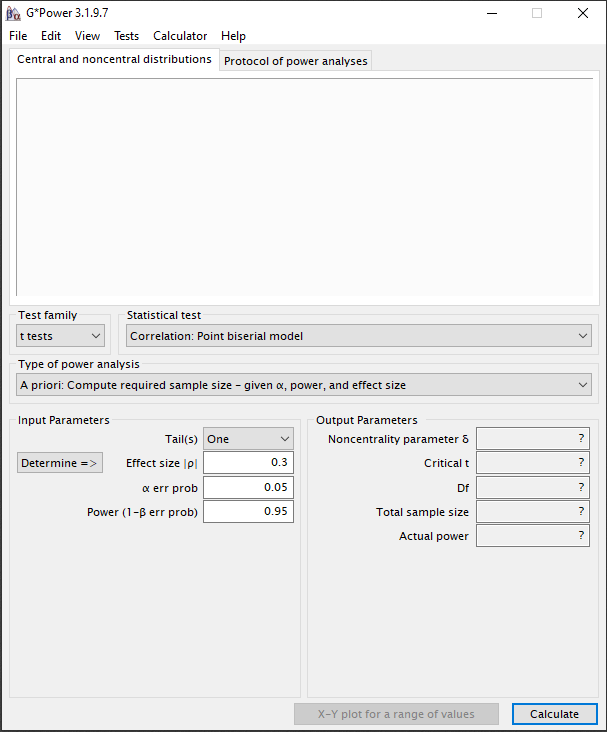
Stap 2:
Aangezien we een meervoudige lineaire regressie willen uitvoeren kiezen we bij de “Test family” de F-test.
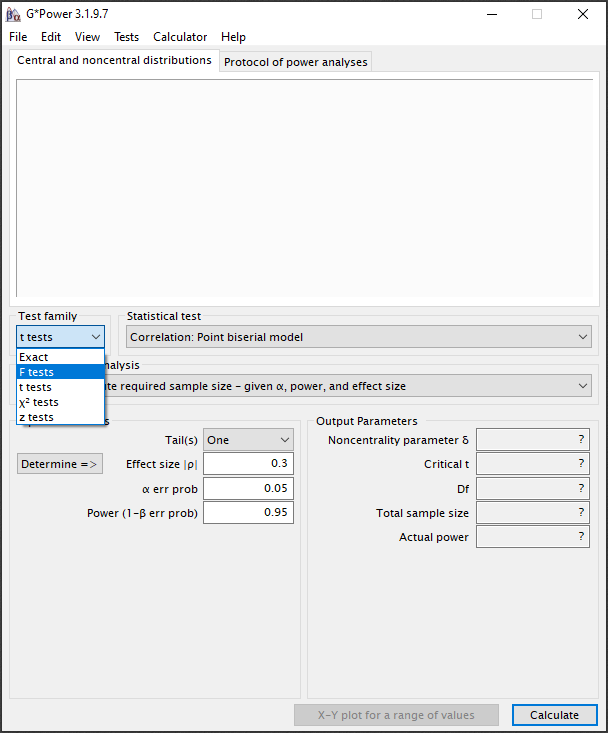
Stap 3:
Bij de “Statistical test” selecteren we “Linear multiple regression: Fixed model, R2 deviation from zero”.
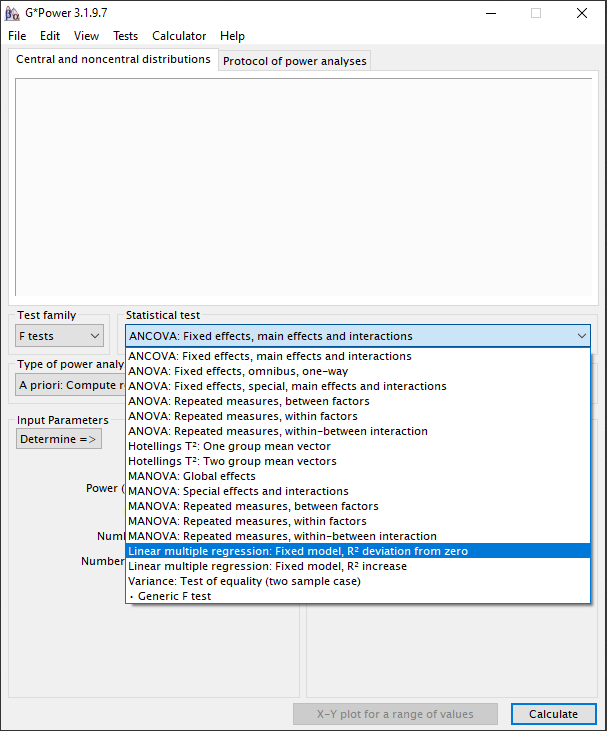
Stap 4:
In G*Power is er niet een directe manier om het aantal variabelen te bepalen. Daarom laten we een “trial and error” manier zien waarmee je het aantal variabelen kan bepalen. Binnen G*Power zijn er twee indirecte manieren om het aantal variabelen te bepalen. De eerste manier is via een sensitivity-test, de tweede manier is via een post-hoc test. Als je voorkeur is dat je de power vooraf bepaalt, dan kies je voor de sensitivity optie. Als je voorkeur is dat je de effect size vooraf bepaalt, dan kies je voor de post-hoc optie. Meestal willen we de type I fout (α) en power (1-β) controleren. De daadwerkelijke meetnauwkeurigheid, gerealiseerde effect size, is dan een gevolg. Dus, laten we met een sensitivity-test beginnen. We selecteren nu bij “Type of power analysis” de optie “Sensitivity: Compute required effect size – given α, power, and sample size”.
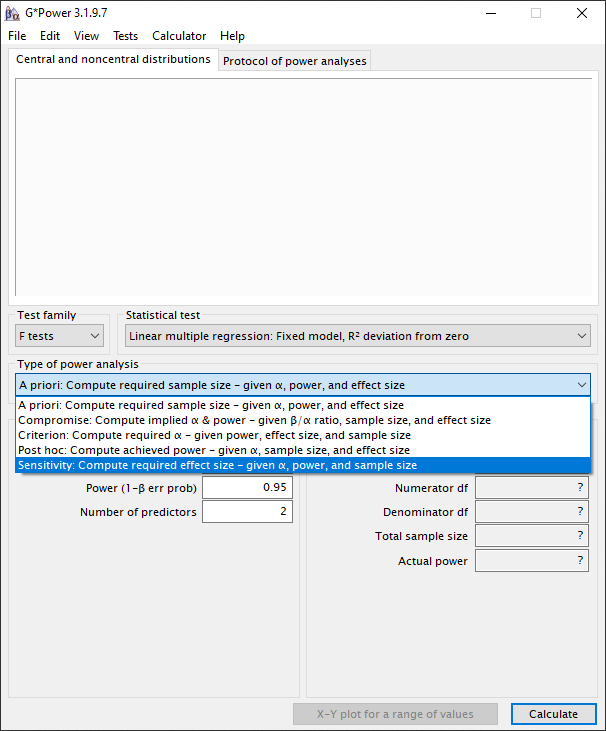
Stap 5:
We stellen de significantie (α) in op 0.05 omdat dit in lijn is met de conventie. De power (1-β) stellen we in op 0.95, hiermee verkleinden we de kans dat we de alternatieve hypothese onterecht verwerpen. De power (1-β) zou je ook op 0.80 kunnen instellen, daarmee kan je kleinere effect sizes meten, meer variabelen meten of je steekproefomvang verkleinen. De consequentie is dan we dat de kans dat je onterecht je alternatieve hypothese verwerpt groter wordt. Cohen (1992, p.156) adviseert een minimum power van 0.80. Hij geeft aan dat een power level van kleiner dan 0.80 resulteert in een onacceptabel hoog risico op een type II fout. Cohen (1992, p.156) geeft aan dat een hoge power resulteert in een groter aantal observaties, misschien meer dan je kan realiseren. Het aantal variabelen stellen we in op 10. De gemiddelde dataset op basis van enquêtes is doorgaans 100 bruikbare response.
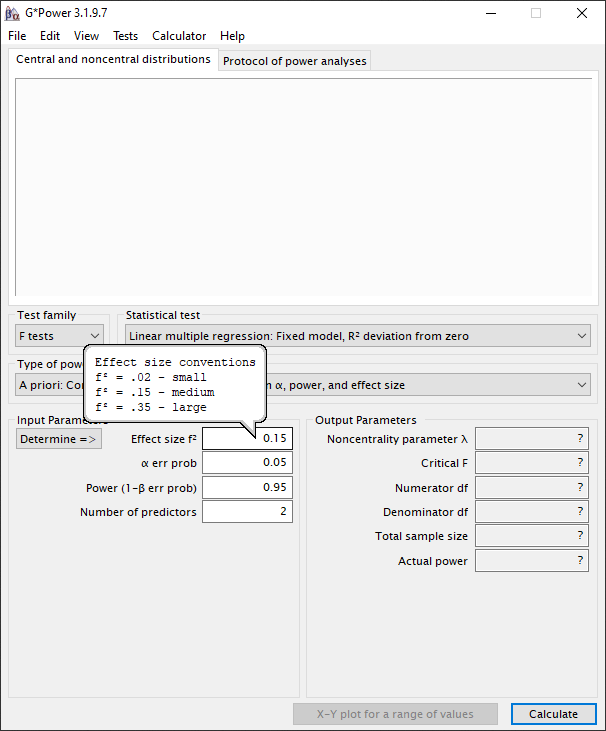
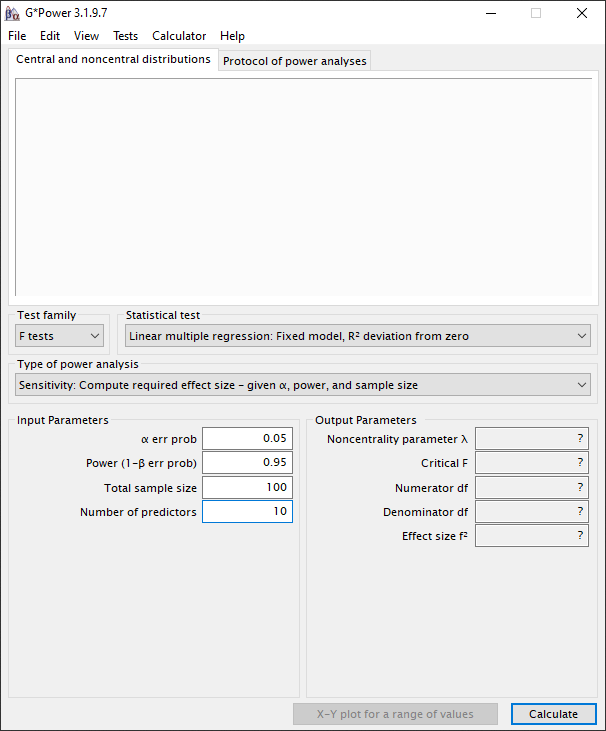
Geïnteresseerd in onze andere Tips? >>
Stap 6:
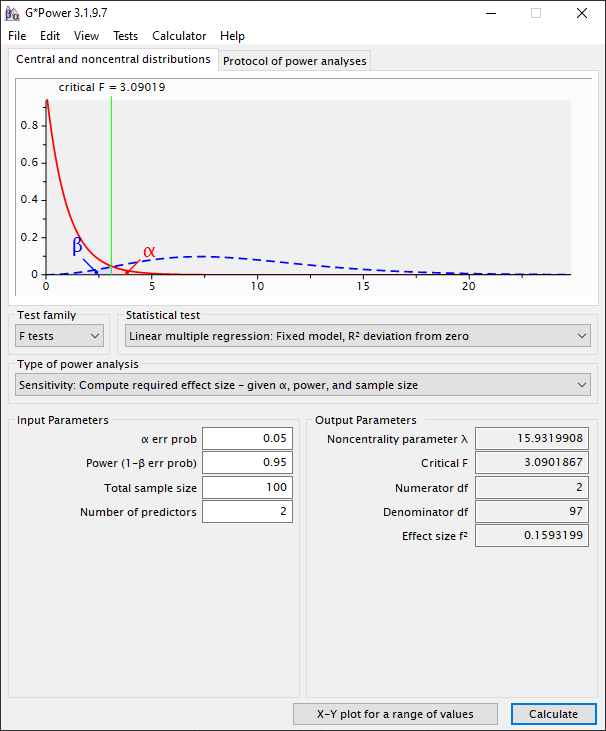
Als we dan op “Calculate” drukken zien we dat de effect size (Cohen’s f2) gelijk is aan 0.27. Dit is in termen van de Cohen’s f2 dus een medium size effect in. Dit wil dus zeggen, als we met deze dataset van 100 observaties en 10 variabelen een meervoudige lineaire regressie gaan uitvoeren dan is het kleinste effect dat we kunnen waarnemen 0.27/(1+0.27) = 0.21. Dit komt dus neer op 21% van de gemeenschappelijke variantie met je afhankelijke variabele.
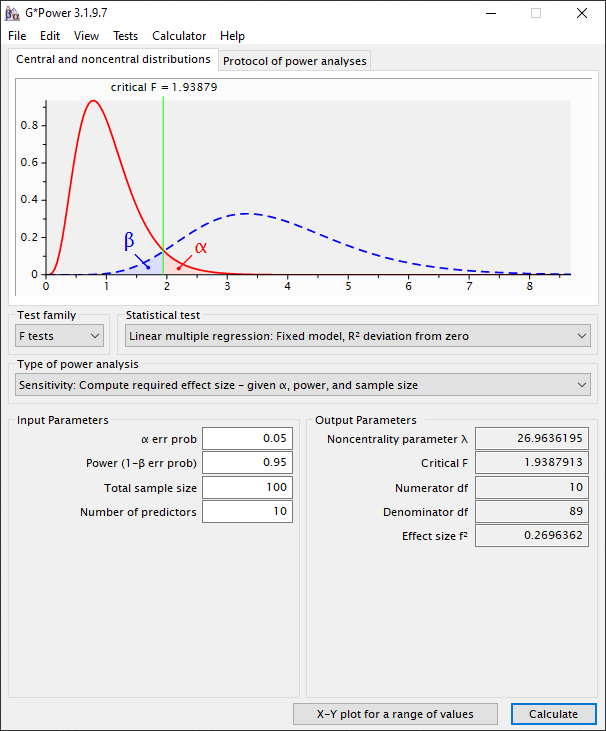
Gewenste effect size in exploratief onderzoek.
Als je in je onderzoek op zoek bent naar een subtiele verandering. In termen van de operationele definitie van Cohen (1988) een “small effect”, als je dus weinig controle hebt over het experiment en met een exploratief onderzoek bezig bent, dan is een f2 van 0.02 meer van toepassing. De consequentie bij tien variabelen is dat de steekproefomvang dan moet toenemen tot 1.229 observaties. Stel dat de steekproefomvang vast staat op 100 observaties, en je geen concessies wil doen aan de α en β waarden, dan heb je nog maar één keuze om de meetnauwkeurigheid te verhogen: het verminderen van het aantal regressievariabelen. Dus, om over-specificatie (overfitting a model) te voorkomen zou je dus maximaal 2 variabelen in je model kunnen opnemen. Het zal niet als een verassing komen dat met 2 variabelen er een grote kans is dat het model onder-gespecificeerd (underfitting a model) is.
Geïnteresseerd in onze andere Tips? >>
Stap 7:
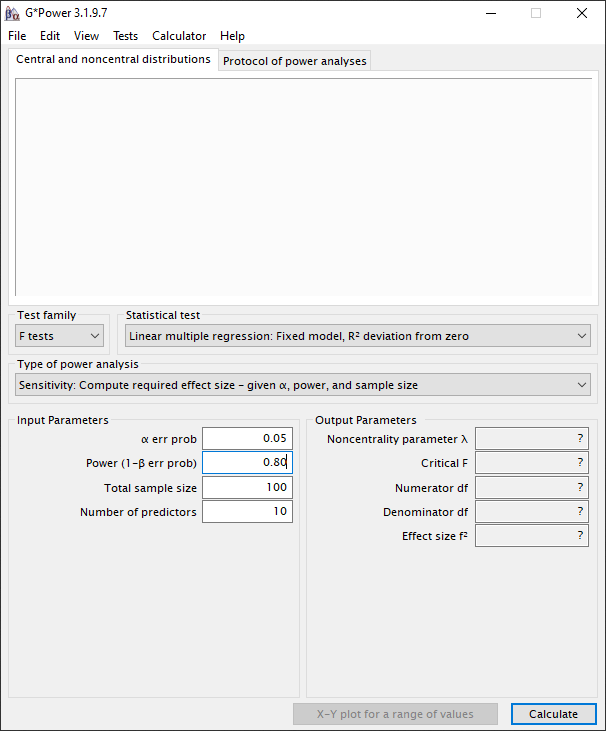
Laten we nu als experiment de power reduceren naar het minimum wat Cohen (1992, p.156) adviseert. We houden alle instellingen gelijk, dus met 10 variabelen, en reduceren de power van 0.95 naar 0.80.
Stap 8:
Als we dan op “Calculate” drukken zien we dat de effect size (Cohen’s f2) gelijk is aan 0.18. Dit is in termen van de Cohen’s f2 dus een medium size effect in. Dit wil dus zeggen, als we met deze dataset van 100 observaties en 10 variabelen een meervoudige lineaire regressie gaan uitvoeren dan is het kleinste effect dat we kunnen waarnemen 0.18/(1+0.18) = 0.15. Dit komt dus neer op 15% van de gemeenschappelijke variantie met je afhankelijke variabele.
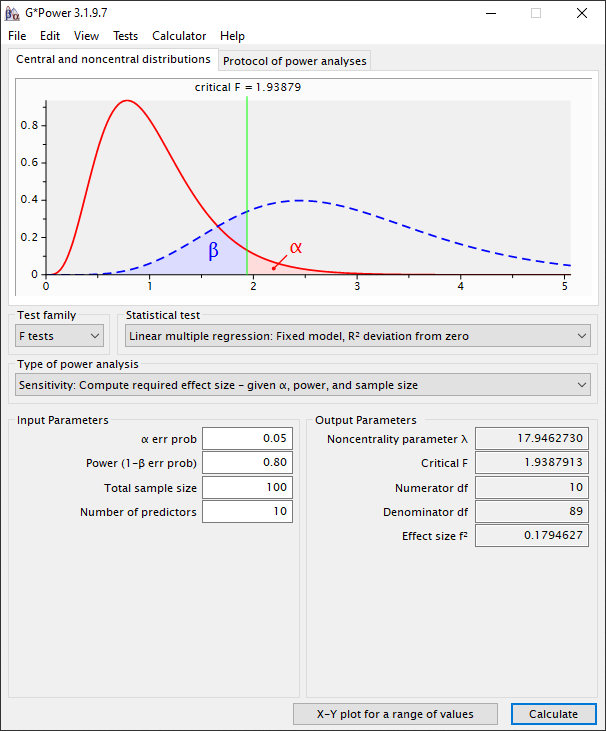
Als je met exploratief onderzoek bezig bent, waarbij je niet voor alle variabelen kan controleren (noise), dan heeft een small effect size de voorkeur. In dit geval zou de doelstelling zijn om de effect size (f2) tussen de 0.02 en 0.15 te kiezen. Als we de effect size (f2) onder de 0.15 willen krijgen, kunnen we in G*Power het aantal variabelen stapsgewijs aanpassen totdat de effect size onder de 0.15 is. In onderstaand voorbeeld wordt duidelijk dat onze dataset bij een power van 0.80 en een effect size van 0.15 maximaal 6 variabelen aan kan.
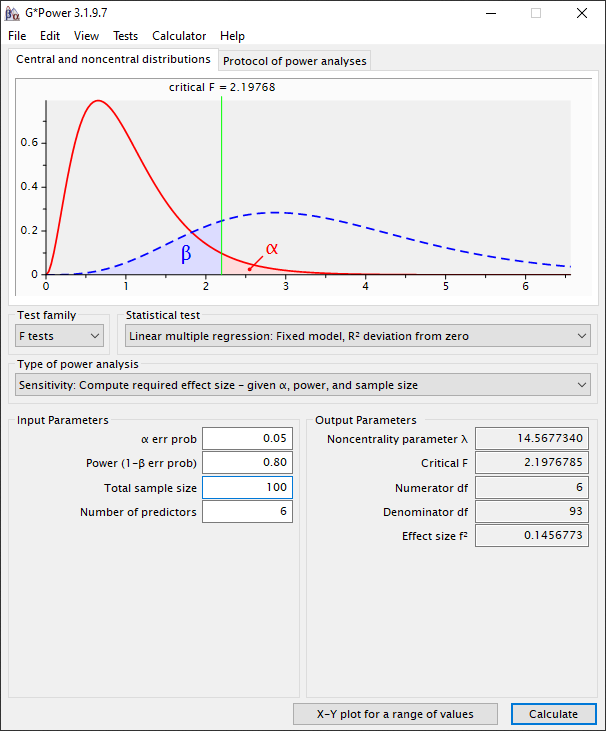
Stap 9:
Zoals beschreven bij stap 4 kunnen we via de post-hoc optie de effect size instellen in plaats van de power. Dus, laten we vervolgen met de post-hoc-test. We selecteren nu bij “Type of power analysis” de optie “Post hoc: Compute achieved power – given α, sample size, and effect size”.
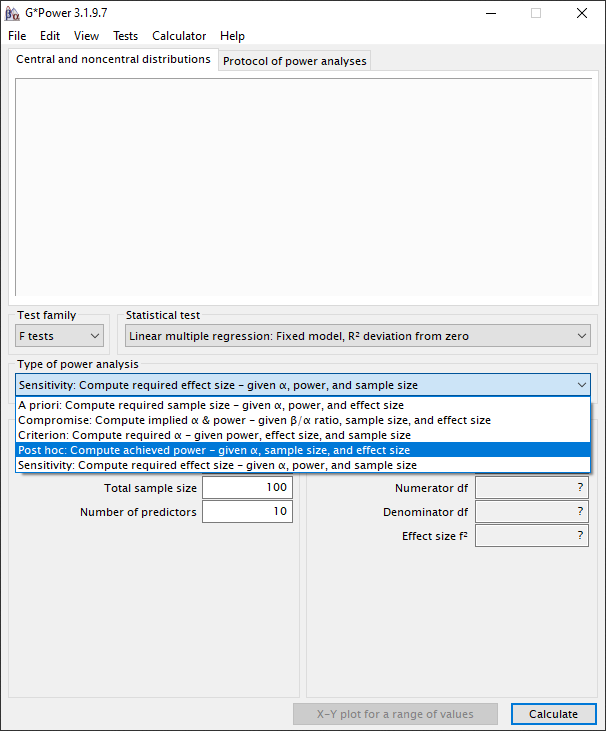
Stap 10:
De instellingen blijven gelijk als eerder aangegeven.
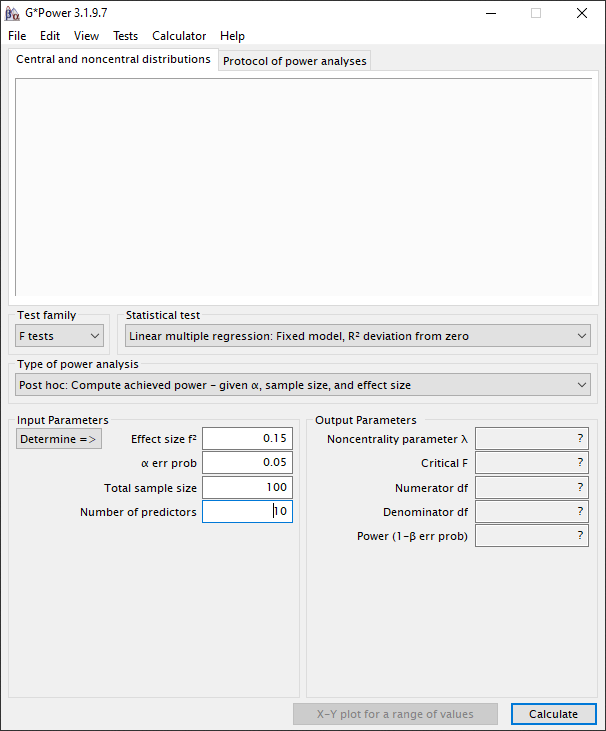
Stap 11:
Als we dan op “Calculate” drukken zien we dat de power gelijk is aan 0.71. Dit bij een medium effect size (Cohen’s f2= 0.15). Dus als er een effect in de data zit ter grootte van 13% (0.15/ (1+0.15)) van de gemeenschappelijke variatie met de afhankelijke variabele, dan hebben we een kans van 71% om die te vinden. Dit is aanzienlijk lager dan de conventie van 80%, 90% of 95% en zal waarschijnlijk door je beoordelaar niet worden geaccepteerd. Hieruit blijkt wederom dat voor dit onderzoek of het aantal observaties moet worden verhoogd of het aantal variabelen moet worden verlaagd.
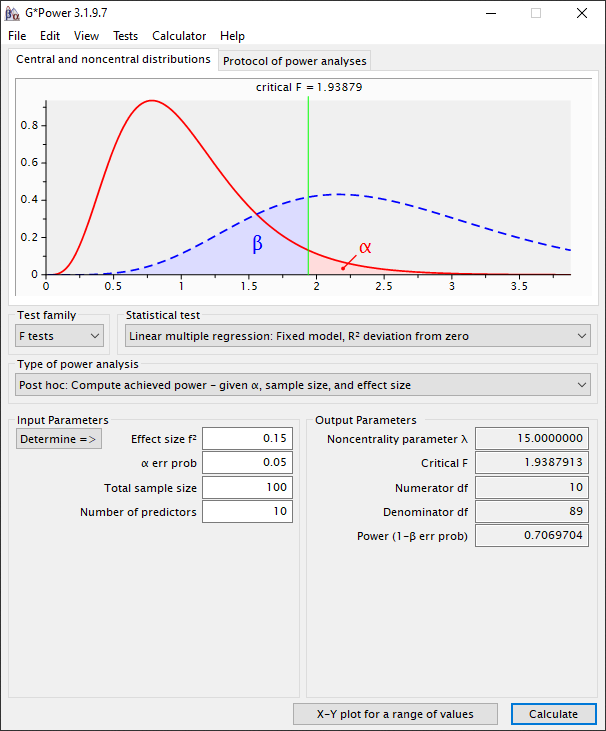
Stap 12:
Nu je kennis gemaakt hebt met G*Power kan je door de “A Priori: Compute required sample size – given α, power, and effect size” te selecteren bij “Type of power analysis” zelf wat experimenteren. Stel dat je de Tabachnick and Fidell (2007, pp. 123-124) zou aanhouden. Hierbij gaan zij er van uit dat α =0.05, β = 0.20 (power is 80%) en een medium effect size (f2 = 0.15). Dan zou je bij hun berekening minimaal 50+8*10 = 130 observaties nodig hebben. De berekening via G*Power laat zien dat je minimaal 118 observaties nodig hebt.
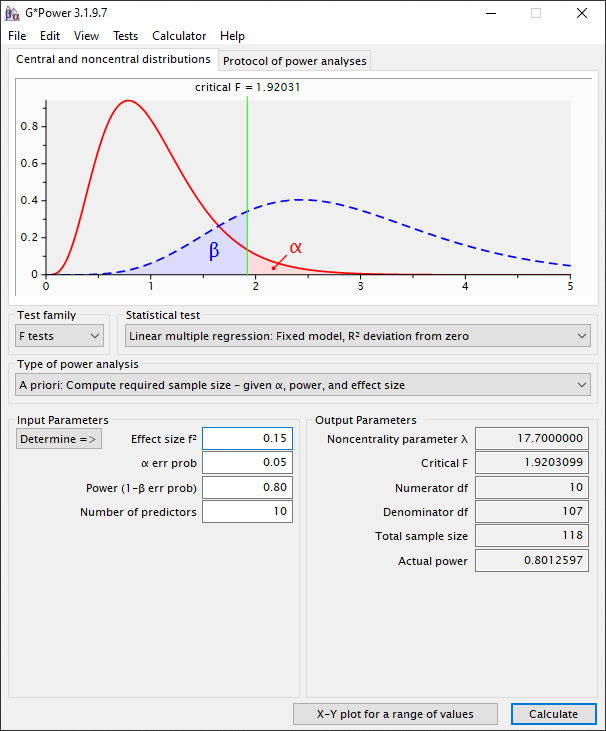
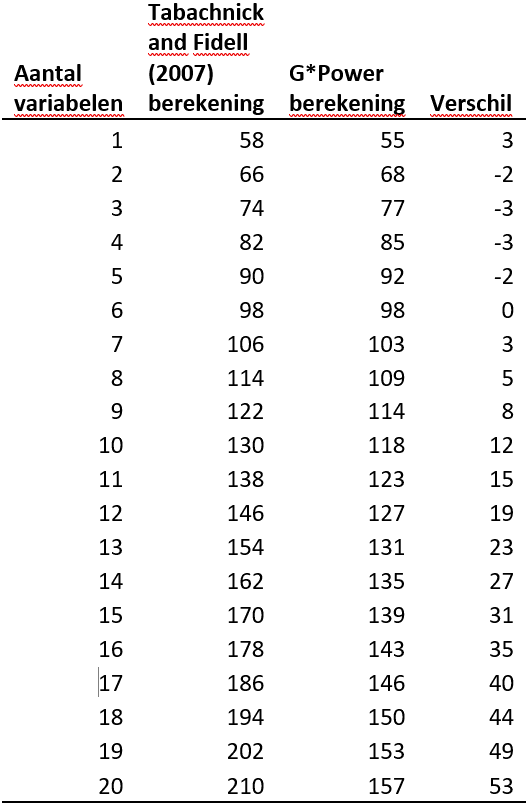
In het begin van deze pagina gaven we aan dat volgens ons G*Power een meer verfijndere methode is om het aantal variabelen en de steekproefomvang te bepalen dan de vuistregel van Tabachnick and Fidell (2007, pp. 123-124). In onderstaande tabel wordt duidelijk dat je met de Tabachnick and Fidell (2007, pp. 123-124) vuistregel tot 6 variabelen te weinig observaties hebt, en boven de 6 variabelen teveel observaties hebt dan strikt noodzakelijk.
Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.
Ben je benieuwd wat onze scriptiebegeleiding (scriptiehulp) je kost? Neem dan een kijkje op onze tarievenpagina via onderstaande button!
Wat kost scriptiebegeleiding? >>
Literatuurlijst:
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2 ed.). New York: Lawrence Erlbaum Associates.
- Tabachnick, B. G., & Fidell, L. S. (2007). Using multivariate statistics (5 ed. Vol. 5). Boston, MA: Pearson Education.