Conceptueel model: Wat is een modererende (conditionele) relatie?
Als je in je scriptie een conceptueel model creëert met een oorzaak-gevolgrelatie (directe relatie) kan het voorkomen dan je deze oorzaak-gevolgrelatie wil testen bij verschillende condities van een andere variabele (moderator). Dit conditionele effect van de directe relatie wordt ook wel een modererend-effect of interactie-effect genoemd. Als we het voorbeeld van de snelheid van de auto er weer bij nemen, dan willen we misschien weten wat het effect is van een verandering van het gaspedaal op de snelheid van de auto als het in de eerste versnelling staat. Maar, naast het conditionele effect van de eerste versnelling wil je ook de invloed van de andere versnellingen weten. Heeft een verandering van het gaspedaal hetzelfde effect op de snelheid in versnelling 1, 2, 3, …etc.? Als je hierin geïnteresseerd bent kijk je dus naar het interactie-effect van de versnelling op de relatie tussen het gaspedaal en de snelheid van de auto.
Voorbeeld conceptueel model met een modererende (conditionele) relatie
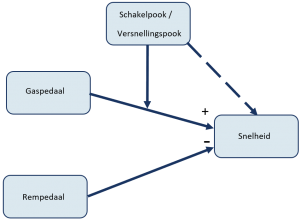
Implementatie van een interactie-effect in een regressieanalyse.
In een regressieanalyse zou je het interactie-effect (conditionele) effect kunnen meten door de variabele die de stand van het gaspedaal weergeeft te vermenigvuldigen met de variabele die de stand van de schakelpook weergeeft. Maar pas wel goed op bij de interpretatie van de resultaten. Als je naast je controlevariabelen alleen het interactie-effect opneemt in je regressieanalyse, kan je geen onderscheid meer maken tussen het directe-effect van het gaspedaal op de snelheid, het directe-effect van de versnellingspook op de snelheid en het interactie-effect van het gaspedaal en versnellingspook op de snelheid. Dus, om het interactie-effect zuiver te meten is het noodzakelijk dat je de hoofdeffecten meeneemt in je regressieanalyse. Daarnaast is het verstandig bij het uitvoeren van de regressieanalyse te controleren op de aannames van de regressie, zoals lineariteit, homogeniteit, multicollineariteit en de onafhankelijkheid van je observaties.
Geïnteresseerd in onze andere Tips? >>De interpretatie van een interactie-effect in een regressieanalyse.
Als je regressieanalyse met een uitkomst is gekomen dan kan het lastig zijn om de resultaten te interpreteren. Zeker als je met interactie-effecten (moderatie-effecten) werkt. Met een interactie-effect kijk je naar de conditionele effecten van je onafhankelijke variabele op je afhankelijke variabele (Hayes, 2013, 2018; Hayes, Glynn, & Huge, 2012). De oorzaak van interpretatieproblemen van een interactie-effect komt doordat het interactie-effect niet los van de hoofdeffecten geïnterpreteerd kan worden. Hierbij is het lastig om te onderscheiden wat nu de invloed van het hoofdeffect en van het interactie-effect is. De meest eenvoudige oplossing is dan om de gecombineerde effecten grafisch te illustreren.
Hulpmiddelen om een interactie-effect grafisch te illustreren
Een interessante tool om het interactie-effect te visualiseren is te vinden op onze pagina “Interpretatie van interactie-effecten door middel van een Excel-plot”. Daarnaast kan je met behulp van de voorbeeld Stata code in het artikel van Meyer, van Witteloostuijn, and Beugelsdijk (2017) de “effect size” van de interactie visualiseren. Een andere optie is om via de “simple slopes” de “marginal effects” te berekenen of een “marginsplot” te maken. Als je informatie zoekt over de “marginal effect” en “marginsplot” bekijk dan eens onze “Wat zijn de marginal effects van een regressie?“ pagina.
Gratis Intakegesprek? >>Kijk ook eens op onze TIPs pagina als je op zoek bent naar informatie over de uitgangspunten van een regressieanalyse.
Wil je hulp bij het gebruik van deze tool, of scriptiebegeleiding bij je regressieanalyse, stel dan vrijblijvend je vraag via WhatsApp of vul ons Contactformulier in.
Literatuurlijst:
- Hayes, A. F. (2013). Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. New York, NY: The Guilford Press.
- Hayes, A. F. (2018). Introduction to mediation, moderation, and conditional process analysis second edition: A regression-based approach (2 ed.). New York: The Guilford Press.
- Hayes, A. F., Glynn, C. J., & Huge, M. E. (2012). Cautions Regarding the Interpretation of Regression Coefficients and Hypothesis Tests in Linear Models with Interactions. Communication Methods and Measures, 6(1), 1-11. doi:10.1080/19312458.2012.651415
- Meyer, K. E., van Witteloostuijn, A., & Beugelsdijk, S. (2017). What’s in a p? Reassessing best practices for conducting and reporting hypothesis-testing research. Journal of International Business Studies, 48(5), 535-551. doi:10.1057/s41267-017-0078-8