Hoe kan je de normaalverdeling van een variabele bepalen met de skewness en kurtosis?

Een standaard onderdeel van je scriptieonderzoek is vaak de rapportage van de beschrijvende data. In dit onderdeel geef je de lezer een algemene indruk van de typische respondent/observatie in je database. Als je bijvoorbeeld na de beschrijvende data een correlatie- of regressieanalyse uit voert dan is de distributie van de residuen van belang voor de berekening van de standaardfout (standaard error), betrouwbaarheidsinterval (confidence interval) en significantie (p-waarde). De berekening van de significantie wordt gedaan op basis van de standaardfout en de t-distributie. Als de residuen dus niet zijn verdeeld conform deze distributie is de significantie van een regressievariabele incorrect.

Wat is het probleem met de formele testen?

Er zijn vele verschillende testen die je zou kunnen doen om de normaal distributie van de residuen te bepalen, onder andere Kolmogorov-Smirnov test, Shapiro-Wilk test, Anderson-Darling test, D’Agostino test en de Jarque-Bera test. De Kolmogorov-Smirnov en de Shapiro-Wilk test zijn de meest gebruikte normaliteit testen op dit vlak. Laten we als voorbeeld de Kolmogorov-Smirnov of een Shapiro-Wilk test nemen. De kritiek van Ghasemi and Zahediasl (2012) op deze testen is dat ze zeer gevoelig zijn voor extreme waarden en de omvang van de dataset. In kleine datasets kunnen deze testen onvoldoende de afwijking van normaal detecteren (low power) (Razali & Wah, 2011), en kunnen ze onterecht aangeven dat een distributie normaal is verdeeld. In grote datasets zijn deze testen overgevoelig voor kleine afwijkingen van normaal en kunnen deze testen onterecht aangeven dat een distributie niet normaal is verdeeld (Kim, 2012, 2013).

Wat is een robuustere manier om de normaalverdeling van de residuen te meten?

Daarom wordt door Kim (2012, 2013) voorgesteld om te werken met de skewness (scheefheid) en kurtosis (gepiektheid/ gewelfdheid / tailedness ) metingen. Maar nu ontstaat het volgende probleem. Welke waarde van de skewness en kurtosis zijn nu acceptabel, met andere woorden, wanneer is de skewness en kurtosis nu goed? Het antwoord hierop is, dat hangt af van de grootte van de dataset.

Voor een dataset van minder dan 300 observaties geld de volgende procedure.

Een handige manier die Kim (2012, 2013) voorstelt is om de gestandaardiseerde skewness en kurtosis te gebruiken. De gestandaardiseerde skewness en kurtosis kan je zelf heel gemakkelijk bereken door in SPSS via de Explore functie (Analyze => Descriptive Statistiscs => Explore) de descriptives van de variabele op te vragen. En dan de skewness te delen door de standaard error van de skewness, en de kurtosis te delen door de standaard error van de kurtosis. Effectief heb je nu de Z-waarden van de skewness en kurtosis berekend. In een Z-waarde tabel zou je nu bij een tweezijdige test de rechter overschrijdingskans kunnen opzoeken voor α/2. In de Z-waarde tabel zie je dat dit 1.96 is. Kortom, als je een gestandaardiseerde skewness of kurtosis hebt van meer dan 1.96 weet je dat deze niet normaal verdeeld is.

Wat zijn Z-waarden?

De Z-waarden zijn onderdeel van een Z-distributie. De Z-distributie is een gestandaardiseerde verwachting hoe vaak je een bepaalde waarde tegenkomt t.o.v. de middelste waarde.  Je verwacht de middelste waarde het meest aan te treffen, en als je verder positief of negatief afwijkt van die middelste waarde verwacht je een lager aantal van die desbetreffende waarde tegen te komen. Het nadeel van de Z-distributie is dat deze onnauwkeurig is bij kleine datasets. Bij datasets van minder dan 30 observaties wordt vaak de t-distributie gebruikt, omdat deze verdeling rekening houdt met een groter aantal (extreme) waarden in de staart van de distributie. De Z-waarden (Z-score) wordt ook vaak gebruikt als indicatie of een distributie normaal is verdeeld.

Kan ik deze richtlijn met elke dataset toepassen?

Maar, één overweging hebben we je nog niet verteld. De standaardfout wordt namelijk lager als het aantal observaties toeneemt. Dit zie je terug in de formule van de standaard error/standaard deviatie.

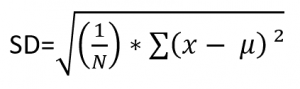
Kleine datasets

Daarom, als de dataset groter wordt kan je gestandaardiseerde skewness of kurtosis ook toenemen. Als gevolg adviseert Kim (2013) om bij kleine dataset (N < 50) Z< 1.96 aan te houden. Kim (2013) adviseert bij dataset tussen 50 en 300 observaties (50 < N < 300) de drempelwaarde van de Z-score te verhogen naar 3.29.

Grote datasets

Voor een dataset van meer dan 300 observaties adviseert Kim (2013)  om de richtlijnen van West, Finch, and Curran (1995) aan te houden.  Zij beargumenteren dat bij datasets van meer dan 300 observaties beter met de niet gestandaardiseerde skewness en kurtosis (Z-scores) kan worden gewerkt, kortom de ruwe waarde. Daarbij adviseren zij een maximale skewness van +/- 2 aan te houden en een maximale kurtosis van 7 (Curran, West, & Finch, 1996).

De kurtosis kan verschillen tussen SPSS, SAS, Excel, R-studio en Stata

SPSS, SAS en Excel

Er zijn verschillende manieren waarop de kurtosis kan worden berekend. Elk statistiek pakket maakt daar zijn eigen keuzes in. SPSS, SAS en Excel gebruiken de formule waarbij de excess kurtosis wordt berekend. Deze statistische softwarepakketten gaan uit van de situatie dat de kurtosis voor een normaal verdeelde variabele (Gauss-kromme ) de waarde heeft van 3. Zij zijn erin geïnteresseerd of er “te veel” of “te weinig” kurtosis aanwezig is. Daarom berekenen zij de overtollige (excess) kurtosis door het getal 3 van de ruwe kurtosis af te trekken. Daar moet je dus wel rekening mee houden bij de evaluatie van de gestandaardiseerde kurtosis als je deze test in een andere applicatie uitvoert. Bijvoorbeeld Stata gebruikt een andere formule en berekend dus niet de excess kurtosis maar de ruwe kurtosis. Aangezien de formules tussen Stata en SPSS van elkaar afwijken zal, bij benadering, de kurtosis in Stata ongeveer met 3 opgehoogd zijn dan in SPSS.

Negatieve waarde van de kurtosis

De ruwe kurtosis heeft een waarde groter of gelijk aan 1. De ruwe kurtosis waarde voor een verdeling die perfect de normaalverdeling volgt heeft de waarde 3. Als je de excess kurtosis berekent kan de waarde van kurtosis dus variëren tussen -2 (1 – 3) en oneindig. Een negatieve excess kurtosis waarde betekend dan dat de verdeling platykurtic is. Een excess kurtosis van 0 betekent dat de verdeling mesokurtic is. En een positieve waarde van de excess kurtosis betekend dat de verdeling leptokurtic is.

De kurtosis formules in SPSS, Stata en R

SPSS

SPSS gebruikt bijvoorbeeld een wat complexere formule die gebaseerd is op de berekening van Sheskin (2000). Het voordeel van deze formule is dat deze een unbiased resultaat oplevert.

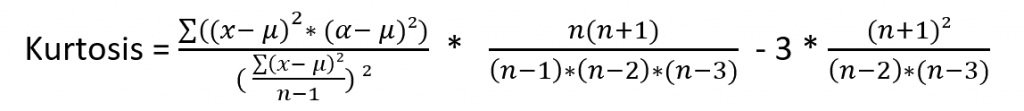
Stata

Stata gebruikt de berekening van Bock (1975) om de kurtosis te berekenen.

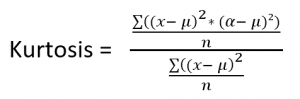
R-Studio

R en R-studio gebruiken de formule op basis van de excess kurtosis.

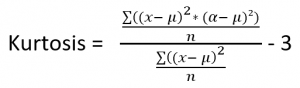
Kurtosis als onderdeel van de centrale momenten

De kurtosis is net als het gemiddelde, variantie en skewness onderdeel van de “method of momements” welke ontwikkeld is door onder andere Pearson (1893). Om een goed basisbegrip te krijgen van de kurtosis is het raadzaam om je eerst te verdiepen in de Methods of Moments (Neyman, 1938; Pearson, 1893). Justin Zeltzer van Z Statistics heeft over de Methods of Moments een zeer intuïtieve en toegankelijke voorlichtingsvideo gemaakt. Klik hier om de video te bekijken. Zijn voorlichtingsvideo over de kurtosis geeft extra inzicht in de kurtosis en zijn beperkingen.

De controversie over de definitie van kurtosis als indicatie van gepiektheid

Deze voorlichtingsvideo legt ook uit dat kurtosis definiëren als de gepiektheid (“peakedness”) van een distributie eigenlijk incorrect is. In de berekening van de kurtosis zit een aanname dat als een distributie een grotere piek krijgt dan een normaalverdeling, deze ook dikkere uitlopers (tails) krijgt.  Kaplansky (1945) heeft aangetoond dat het gebruik van de kurtosis als een meting van gepiektheid onvolledig en misschien wel incorrect is. Dit komt doordat extreme waarde een zeer grote invloed hebben in de formule van de kurtosis. Daarom is het volgens Westfall (2014) een indicatie van een “heavy-tailed” (positieve excess kurtosis) “light tailed” (negatieve excess kurtosis) distributie.

Het debat met betrekking tot de interpretatie van de kurtosis.

Dit perspectief wordt door enkele auteurs bestreden. Zij argumenteren dat de originele artikelen van Pearson (1893) onjuist zijn geïnterpreteerd. Diverse auteurs hebben echter aangeven dat de kurtosis moet worden beschouwd als een combinatie meting van zowel de gepiektheid als de uitlopers (Crack, 2019; DeCarlo, 1997). Darlington (1970) definieert de kurtosis echter als een lage bimodaliteit als de kurtosis hoog is, en er dus maar een piek is. Daarentegen definieert Darlington (1970) een hoge binmodaliteit als de kurtosis laag is, en er dus twee pieken in de verdeling zitten. Kurtosis high = low bimodality kurtosis low = high bimodality.

Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.

Contact! >>     WhatsApp Ons! >>

Ben je benieuwd wat onze scriptiebegeleiding (scriptiehulp) je kost? Neem dan een kijkje op onze tarievenpagina via onderstaande button!

Wat kost scriptiebegeleiding? >>

Literatuurlijst:

1. Bock, R. D. (1975). Multivariate statistical methods in behavioral research. New York: McGraw-Hill.
2. Crack, T. F. (2019). Kurtosis as peakedness: the phoenix from the ashes. Foundations for Scientific Investing.
3. Curran, P. J., West, S. G., & Finch, J. F. (1996). The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychological Methods, 1(1), 16-29.
4. Darlington, R. B. (1970). Is Kurtosis Really “Peakedness?”. The American Statistician, 24(2), 19-22. doi:10.2307/2681925
5. DeCarlo, L. T. (1997). On the meaning and use of kurtosis. Psychological Methods, 2(3), 292-307. doi:10.1037/1082-989X.2.3.292
6. Ghasemi, A., & Zahediasl, S. (2012). Normality tests for statistical analysis: a guide for non-statisticians. International journal of endocrinology and metabolism, 10(2), 486-489. doi:10.5812/ijem.3505
7. Kaplansky, I. (1945). A Common Error concerning Kurtosis. Journal of the American Statistical Association, 40(230), 259-259. doi:10.1080/01621459.1945.10501856
8. Kim, H.-Y. (2012). Statistical notes for clinical researchers: assessing normal distribution (1). Restorative dentistry & endodontics, 37(4), 245-248. doi:10.5395/rde.2012.37.4.245
9. Kim, H.-Y. (2013). Statistical notes for clinical researchers: assessing normal distribution (2) using skewness and kurtosis. Restorative dentistry & endodontics, 38(1), 52-54. doi:10.5395/rde.2013.38.1.52
10. Neyman, J. (1938). A Historical Note on Karl Pearson’s Deducation of the Moments of the Binomial. Biometrika, 30(1/2), 11-15. doi:10.2307/2332220
11. Pearson, K. (1893). Asymmetrical Frequency Curves. Nature, 48(1252), 615-616. doi:10.1038/048615a0
12. Razali, N. M., & Wah, Y. B. (2011). Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. Journal of Statistical Modeling and Analytics Vol, 2(1), 21-33.
13. Sheskin, D. J. (2000). Handbook of Parametric and Nonparametric Statistical Procedures Chapman (2 ed.). Chapman & Hall/CRC: Boca Raton, Florida.
14. West, S. G., Finch, J. F., & Curran, P. J. (1995). Structural equation models with nonnormal variables: Problems and remedies. In R. H. Hoyle (Ed.), Structural equation modeling: Concepts, issues, and applications. (pp. 56-75). Thousand Oaks, CA, US: Sage Publications, Inc.
15. Westfall, P. H. (2014). Kurtosis as Peakedness, 1905–2014. R.I.P. The American Statistician, 68(3), 191-195. doi:10.1080/00031305.2014.917055

Geïnteresseerd in onze andere Tips? >>