Wat zijn de marginal effects van een regressie interactie-effect?

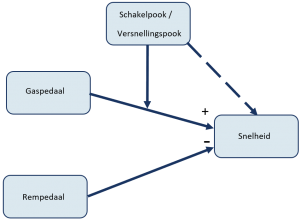
Een marginal effect kijkt naar de invloed van een onafhankelijke variabele op een afhankelijke variabele waarbij alle andere (controle) variabelen constant worden gehouden. Als voorbeeld kunnen we de onderstaande regressieformule analyseren.

Snelheid = (3-30) + 60 * stand gaspedaal + 30 * stand versnellngspook+ 10 *  stand gaspedaal * stand versnellingspook

We verminderende constante met 30 omdat een handmatige versnelling geen neutraal (0) stand heeft.

Dit zou betekenen dan in de eerste versnelling kan je accelereren van 3 tot 63 kph. In de tweede versnelling kan je accelereren van 33 kph tot 103 kph. In de derde versnelling kan je accelereren van 63 kph tot 143 kph.

Een marginal effect is daarom dus de waarde van de afhankelijke variabele bij een specifieke combinatie van onafhankelijke variabele en mediator. Dus met behulp van de coëfficiënten van je regressie en het gemiddelde en de standaardfout van je variabelen zou je de marginal effecten handmatig kunnen uitrekenen.

Zijn er hulpfuncties in SPSS en/of Stata om de marginal means uit te rekenen?

In Stata is er een heel handige functie die je kan helpen om de marginal effect uit te rekenen, deze functie heet heel toepasselijk “margins”. Met behulp van deze “margins” functie kan je de datapunten genereren voor de margins pIot. Daarnaast zou je de functie “predictnl” in Stata kunnen gebruiken na het schatten van je regressie coëfficiënten om de datapunten voor je simple slope te genereren (Meyer, van Witteloostuijn, & Beugelsdijk, 2017). In SPSS is er op het moment van het schrijven van deze pagina nog geen handige functie op de marginal effect uit te rekenen of te plotten.

Hoe bereken je een simple slope?

Bij het berekenen van de “simple slopes” (marginal effect) is relatief eenvoudig uit te voeren. Stel dat onze regressieformule er als volgt uit ziet.

• Y = β₀ + β₁ * X + β₂ * M + β₃ * X * M

Hierbij zijn:

Y : Afhankelijke variabele

X : Onafhankelijke variabele

M: Moderator

β₀ : Constante

Het herschrijven van de regressieformule

Dan bereken we de simple slope, dus de conditionele effecten van X op Y, door eerst de X te isoleren. In essentie zijn formule (1) en (2) gelijk aan elkaar, alleen anders opgeschreven.

• Y = (β₀ + β₂ * M ) + X * (β₁ + β₃ * M)

Het gedeelte “(β₀ + β₂ * M )“ geeft de simple intercept aan, dit meet de waarde van de afhankelijke variabele als de onafhankelijke variabele nul is.  Het gedeelte “X * (β₁ + β₃ *  M)“ geeft de simple slope van de onafhankelijke variabele aan bij diverse condities van de moderator variabele. De simple slope laat zien welke waarde de afhankelijke variabele aanneemt bij verschillende waarde van de onafhankelijke en moderator variabele. De conventie is dat de waarde van de afhankelijke variabele wordt berekend bij plus en min 1 standaarddeviatie van de onafhankelijke en moderator variabele (Dawson, 2014; Dawson & Richter, 2006; Liu, West, Levy, & Aiken, 2017).

Kritiek op de huidige berekening van de simple slope

Het berekenen van de simple slope op basis van plus en min 1 standaard deviatie word bekritiseerd door Meyer et al. (2017). Zij beargumenteren dat het maken van een regressie interactieplot waarbij de lijnen zijn gebaseerd op plus en min 1 standaarddeviatie onvolledig is. Hun kritiek is dat deze methode de onzekerheid, lees hier het 95% betrouwbaarheidsinterval, negeert. Tevens kan het goed zijn dat plus en min 1 standaarddeviatie niet representatief is voor alle mogelijke waarden. Meyer et al. (2017) geven in hun bijlage een voorbeeld Stata-code om de effect size van een interactie weer te geven, en laten in hun artikel zien hoe deze geïnterpreteerd moet worden. Om deze plot en de interpretatie van de plot representatief te houden adviseren Liu et al. (2017) om gedeelte waar er (bijna) geen datapunten zijn, bijvoorbeeld vanwege de scheefheid van de distributie, niet af te beelden.

Kijk ook eens op onze TIPs pagina als je op zoek bent naar informatie over de uitgangspunten van een regressieanalyse.

Wil je hulp bij het gebruik van deze tool, of scriptiebegeleiding bij je regressieanalyse, stel dan vrijblijvend je vraag via WhatsApp of vul ons Contactformulier in.

WhatsApp Ons!   Contact

Literatuurlijst:

1. Dawson, J. F. (2014). Moderation in Management Research: What, Why, When, and How. Journal of Business and Psychology, 29(1), 1-19. doi:10.1007/s10869-013-9308-7
2. Dawson, J. F., & Richter, A. W. (2006). Probing three-way interactions in moderated multiple regression: Development and application of a slope difference test. Journal of Applied Psychology, 91(4), 917-926. doi:10.1037/0021-9010.91.4.917
3. Liu, Y., West, S. G., Levy, R., & Aiken, L. S. (2017). Tests of Simple Slopes in Multiple Regression Models with an Interaction: Comparison of Four Approaches. Multivariate Behavioral Research, 52(4), 445-464. doi:10.1080/00273171.2017.1309261
4. Meyer, K. E., van Witteloostuijn, A., & Beugelsdijk, S. (2017). What’s in a p? Reassessing best practices for conducting and reporting hypothesis-testing research. Journal of International Business Studies, 48(5), 535-551. doi:10.1057/s41267-017-0078-8