Multicollineariteit in een regressieanalyse
Figuur 1
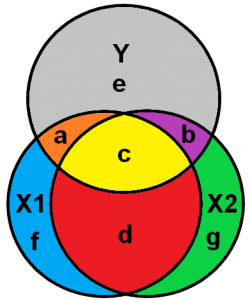
In een regressieanalyse wil je het “zuivere” effect van een onafhankelijke variabele op een afhankelijke variabele meten. Daarom wordt de gemeenschappelijke variantie (gebied c in figuur 1) uit de variabelen verwijderd. In dit geval ontstaat er een verschil tussen de correlatiecoëfficiënt en de gestandaardiseerde beta in de regressie (Thompson, 2006, pp. 233-237). Dus, op het moment dat er multicollineariteit is, kan je er niet meer van uit gaan dat je correlatiecoëfficiënt overeenkomt met je regressiecoëfficiënt.
Waarom is multicollineariteit nu een probleem?
Multicollineariteit is een probleem omdat de gemeten standaard error van je regressie hoger is dan deze in werkelijkheid zou moeten zijn. Als de standaard error groter wordt, wordt daarmee ook je p-waarde groter en dus je resultaat minder significant. Met andere woorden, je risico op een type II fout wordt hoger omdat je de onware nulhypothese niet verwerpt (Grewal, Cote, & Baumgartner, 2004). Daarnaast wordt de regressiecoëfficiënt gebaseerd op minder variatie en daardoor minder nauwkeurig (onstabiel). Namelijk, het gele vlak (c) (Figuur 1) wordt verwijderd uit de analyse omdat we alleen geïnteresseerd zijn in de unieke “zuivere” effecten. Bij benadering zou je kunnen inschatten dat voor X1 het verlies door multicollineariteit gelijk is aan ry*x1 * rx1*x2. In het geval van ernstige multicollineariteit wordt het moeilijk voor de regressie om de individuele effecten van X1 op Y en X2 op Y van elkaar te onderscheiden.
Het effect van multicollineariteit geïllustreerd via een Ballentine diagram (Venn-diagram)
Figuur 2
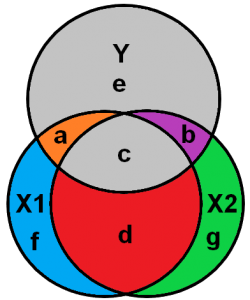
Hierbij blijkt ook dat het grijze gebied ( e), welke de standaard error van de regressie illustreert, groter wordt (Figuur 2) ondanks dat er een extra variabele is toegevoegd ( e + c). De standaard error voor X1 kan benaderd worden door het grijze gebied Y ( e + c ) gedeeld door a + f. Doordat a + f kleiner is geworden, en e is toegenomen met c, neemt de standaard error toe.
Geïnteresseerd in onze andere Tips? >>
Hoe kan je testen voor multicollineariteit?
Je kan mogelijke multicollineariteit problemen als eerste ontdekken in je correlatiematrix. Een hoge correlatie tussen twee variabelen kan duiden op een multicollineariteit probleem. De drempelwaarde voor de correlatie hangt een af van welk boek of artikel je gebruikt. Saunders, Lewis, and Thornhill (2016, p. 548) en Tabachnick and Fidell (2007, p. 90) geven aan dat een correlatie van 0,90 of hoger een indicatie is van multicollineariteit. Berry et al. (1985, p. 43) hanteert een correlatie van 0,80 als een indicatie van multicollineariteit. Berry et al. (1985, p. 43) waarschuwt dat afhankelijk van het aantal observaties deze drempelwaarde kan dalen naar 0,7. Berry et al. (1985, p. 43) geeft aan dat de beste manier om multicollineariteit te ontdekken is je afhankelijke variabele te vervangen door een van de onafhankelijke variabelen en dan een regressie uit te voeren. En dit herhaal je voor alle onafhankelijke variabelen. Vervolgens inspecteer je de R-squared van je regressie.
Multicollinairiteit inspectie op basis van de VIF-waarden
Daarnaast kan je de Variation Inflation Factor (VIF) van je regressie controleren. In SPSS vraag je in de opties om de collinairity diagnostics. In Stata kan je na je regressie door middel van het commando estat vif de VIF-waarden controleren. Een VIF-waarde die hoger is dan 10 wordt gezien als een hoge multicollineariteit welke moet worden opgelost. Daarentegen Rogerson (2019, p. 304) geeft aan dat een VIF-waarde van 5 al een teken is van multicollineariteit.
Kritiek op de arbitrair opgestelde vuistregels voor de VIF-waarde
O’Brien (2007) waarschuwt dat de vuistregels voor de VIF-waarde kritisch moeten worden geëvalueerd. Hij beschrijft dat er een verband is tussen de verlaging van de variantie en de verhoging van de steekproefomvang. Als de steekproef groter wordt, dan wordt in verhouding de variatie kleiner en daarmee de kans op multicollineariteit (type II fout). Daarnaast, als de gemeenschappelijke verklaring (R-squared) van alle variabelen in je model groter wordt, blijft er een kleiner deel onverklaarde variantie van de afhankelijke variabele over (grijze gebied “e” in bovenstaande figuur). Dit reduceert de variantie in alle variabelen. O’Brien (2007) geeft aan dat de steekproefomvang en het onverklaarde gedeelte van de variantie in de afhankelijke variabele een wisselwerking met elkaar hebben. Daarom verhoogt je VIF de variantie in de variabele maar reduceert de steekproefomvang en de R-squared de variantie in de variabele. Kortom, de VIF-waarde moet in samenspel met de steekproefomvang en R-squared worden beoordeeld.
Aanvullende kritiek op de vuistregels voor de VIF-waarde
Vatcheva, Lee, McCormick, and Rahbar (2016) laten zien dat het risicovol is om op basis van arbitrair opgestelde vuistregels te bepalen of er sprake is van multicollineariteit. Zij verwijzen naar Freund, Wilson, and Sa (2006, pp. 191-192) en adviseren om de VIF-waarden te vergelijken met de ratio (1 / (1 – R-squared2)). Als de VIF-waarde hoger zijn dat deze ratio is er ernstige multicollineariteit.
Het testen van collineariteit op basis van de condition index
Een andere mogelijkheid die Vatcheva et al. (2016) naar voren brengen is om de Condition Index en de Variance Proportions te controleren. Volgens Belsley, Kuh, and Welsch (2005) kan er onderscheid gemaakt worden tussen degrading collinearity en harmful collinearity. Zij beschouwen degrading collinearity wanneer twee of meer variabelen nog maar de helft van hun sterkte hebben (coëfficiënt) t.o.v. een situatie zonder multicollineariteit (Belsley et al., 2005, p. 117). Vervolgens kan er naast degrading collinearity ook nog harmful collinearity aanwezig zijn. Harmful collinearity is wanneer een van de variabelen het verkeerde teken heeft t.o.v. de situatie zonder multicollineariteit. Belsley et al. (2005) geven aan dat een condition index van meer dan 30 een indicatie is van multicollinearititeit. Daarnaast, als twee of meer variabelen een variance proportion hebben van 0,5 of hoger dan is er tussen die variabelen waarschijnlijk een hoge lineaire afhankelijkheid.
Hoe kan je testen of het teken is omgedraaid vanwege multicollineariteit?
Harmful collinearity betekent dat niet alleen de sterkte van het effect niet correct is, maar ook dat de richting van het effect onjuist is. Hoe ontdek je nu of je alleen met degrading collinearity te maken hebt of met harmful collinearity? De meest eenvoudige manier is om de literatuur over je onderwerp te raadplegen. Als meerdere artikelen een positief effect aantonen en jij meet een negatief effect dan heb je waarschijnlijk harmful collinearity. Daarnaast zou je een principal components regression (Liu, Kuang, Gong, & Hou, 2003) of een ridge regression kunnen uitvoeren om het teken te controleren.
Zijn er verschillende vormen van multicollineariteit?
Er zijn twee vormen van multicollineariteit, “structural multicollinearity” en “data based multicollinearity”. Structurele multicollineariteit ontstaat wanneer je op basis van twee of meer variabelen een nieuwe variabele creëert. Bijvoorbeeld, als je op basis van variabele X1 en variabele X2 een interactievariabele X1*X2 maakt. Een ander veel voorkomende bron van structurele multicollineariteit kan bijvoorbeeld zijn als je een curve-lineair effect wil creëren. Denk aan een u-vorm of een inverse u-vorm van een variabele. Dan voeg je bijvoorbeeld variabele X1 en X12 toe aan je regressieanalyse. Aangezien X12 de vermenigvuldiging is van X1*X1 voeg je twee keer een vergelijkbare variabele toe aan de regressie. Data gebaseerde multicollineariteit ontstaat als twee of meer variabelen veel gemeenschappelijk hebben. Dit kan meestal worden toegewezen aan een onverstandige variabele keuze.
Hoe kan je multicollineariteit oplossen?
De voor de hand liggende keuze is om (aanzienlijk) meer data te verzamelen. Met meer observaties wordt doorgaans je standaardfout kleiner. Hierbij wordt ervan uitgegaan dat je variabelen niet perfect multicollineair zijn. Als je variabelen wel perfect multicollineair zijn dan is meer data verzamelen geen oplossing. Daarentegen je te maken hebt met structurele multicollineariteit kan het mean-centeren of het standaardiseren (SPSS / Stata) van de variabelen helpen. Als je data gebaseerde multicollineariteit hebt is vaak de meest voor de hand liggende oplossing om een van de twee variabelen te verwijderen. Als meer data verzamelen het probleem niet oplost of niet mogelijk is, dan is de meest voor de hand liggende oplossing om op basis van de literatuur meer variabelen toe te voegen aan het model. Hierdoor kan de verklarende waarde van het model worden verhoogd en het effect van multicollineariteit worden verlaagd (York, 2012).
Alternatieve methoden om multicollineariteit te verminderen
De techniek van het “residualization” is omstreden omdat deze de bias in je regressie verhoogd (York, 2012). Een vergelijkbaar argument geld voor ridge regression, ridge regression introduceert een bias in je regressie om de variantie te verminderen. Een ridge regression wordt daarom toegepast als alle andere opties niet werken. Als laatste zou je doormiddel van een principal components analysis de multicollineaire regressors kunnen samenvoegen. Hierdoor neem je de effecten van beide regressors mee, maar reduceer je deze in een kleinere orthogonale set van regressors.
Kijk ook eens op onze TIPs pagina als je op zoek bent naar meer informatie.
Zoek je hulp bij een van de onderdelen van je scriptieonderzoek, stel dan vrijblijvend je vraag via WhatsApp of vul ons Contactformulier in.
Ben je benieuwd wat onze scriptiebegeleiding (scriptiehulp) je kost? Neem dan een kijkje op onze tarievenpagina via onderstaande button!
Wat kost scriptiebegeleiding? >>
Literatuurlijst:
- Belsley, D. A., Kuh, E., & Welsch, R. E. (2005). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New Jersey: Wiley.
- Berry, W. D., Feldman, S., & Stanley Feldman, D. (1985). Multiple regression in practice. Thousand Oaks, California: Sage.
- Freund, R. J., Wilson, W. J., & Sa, P. (2006). Regression Analysis. London: Elsevier Science.
- Grewal, R., Cote, J. A., & Baumgartner, H. (2004). Multicollinearity and Measurement Error in Structural Equation Models: Implications for Theory Testing. Marketing Science, 23(4), 519-529.
- Liu, R. X., Kuang, J., Gong, Q., & Hou, X. L. (2003). Principal component regression analysis with spss. Computer Methods and Programs in Biomedicine, 71(2), 141-147.
- O’Brien, R. M. (2007). A Caution Regarding Rules of Thumb for Variance Inflation Factors. Quality & Quantity, 41(5), 673-690.
- Rogerson, P. A. (2019). Statistical methods for geography: a student’s guide (5 ed.). Thousand Oaks, California: Sage Publications Limited.
- Saunders, M., Lewis, P., & Thornhill, A. (2016). Research methods for business students (Vol. Seventh) (7 ed.). Harlow: Pearson Education
- Tabachnick, B. G., & Fidell, L. S. (2007). Using multivariate statistics (5 ed. Vol. 5). Boston, MA: Pearson Education.
- Vatcheva, K. P., Lee, M., McCormick, J. B., & Rahbar, M. H. (2016). Multicollinearity in regression analyses conducted in epidemiologic studies. Epidemiology (Sunnyvale, Calif.), 6(2), 227.
- York, R. (2012). Residualization is not the answer: Rethinking how to address multicollinearity. Social Science Research, 41(6), 1379-1386.