Het meetniveau van variabelen in je scriptie
In veel scripties of onderzoeken worden variabelen gebruikt als operationalisering van theoretisch concepten/ conceptueel model. Deze variabelen worden uitgedrukt in een meetbare eenheid en/of indicator dat een representatie van het theoretisch concept. Deze operationalisatie doe je doorgaans op basis van de relevante theorie om de betrouwbaarheid en validiteit van de operationalisatie te waarborgen. Daarna wordt het belangrijk om over het meetniveau van de variabele na te denken. Het meetniveau is een belangrijke overweging omdat dit bepalend is welke (statistische) bewerkingen op de variabele zijn uit te voeren en de nauwkeurigheid (hoeveelheid informatie) waar mee gemeten kan worden.
Kwalitatieve variabelen:
Kwalitatieve (attributieve) variabelen zijn variabelen die zijn gebaseerd op namen. Bijvoorbeeld, een dier, of een diersoort, geslacht, kleur, kompasrichting of academisch niveau.
Catogorische schaal (categorical)
Binaire/Dichotome schaal
Een binaire (binary/dichotomous) schaal meet een variabele maar op 2 niveaus, als je ingedeeld wordt op een binaire schaal behoor je of tot de ene of tot de andere categorie. Een bekend voorbeeld is daarvan geslacht, je ben of een man of een vrouw, er zijn geen andere mogelijkheden. Een verbijzondering van een binaire variabele is een dummy variabele die hieronder wordt uitgelegd.
Dummy variabele
Een dummy variabele is wat de titel eigenlijk al suggereert de “domste” variabele die je in je variabelen arsenaal hebt. Een dummy variabele heeft maar twee niveaus, een 0 of een 1. Door dat deze variabele maar twee niveaus kan onderscheiden zit er maar heel weinig variatie in deze variabele en is het een relatief grove meting. Als je bijvoorbeeld je variabele geslacht transformeert naar een dummy variabele, zou je deze eigenlijk moeten hernoemen naar “man” of “vrouw”. Stel dat we “man” kiezen, dan is deze variabele dus “1” als het een “man” is. Als deze variabele “man” een waarde “0” heeft, weten we maar een ding zeker, het is geen man.
Nominale schaal
Een nominale (nominal) schaal is een uitbreiding op de binaire schaal waarbij je net als de binaire schaal verschillende categorieën hebt, maar bij deze variabele kan je meerdere categorieën hebben. Wat een nominale schaal kenmerkt is dat er 2 of meer categorieën zijn die elkaar wederzijds uitsluiten. Dit wil zeggen een observatie mag niet in 2 of meer categorieën geplaatst kunnen worden. Daarnaast kenmerkt een nominale schaal zich doordat de categorieën geen verband of hiërarchische (natuurlijke ordening) bevatten. Een geslacht, kleur, kompasrichting, diersoorten, postcode of je studentnummer zou je kunnen beschouwen als een nominale variabele. Want een hoger postcodenummer of een hoger studentnummer zegt helemaal niets in verhouding met een lager nummer. Een postcode identificeert alleen maar een locatie en studentnummer identificeert alleen maar een persoon. Postcode 3333 is niet 3x beter dan postcode 1111.
De eigenschappen van de nominale schaal
Binnen een nominale variabele kunnen we niet het midden van een distributie bepalen omdat er geen natuurlijke ordening (rangorde) tussen de categorieën zit. Daarom meten we bij een nominale variabele niet het midden van de distributie maar de waarde die het meeste voorkomt. De waarde die het meeste voorkomt wordt de modus genoemd.
Ordinale schaal
Een ordinale (ordinal) schaal heeft veel overeenkomsten met een nominale schaal, hiermee bedoelen we dat het bestaat uit 2 of meer categorieën. Het speciale aan een ordinale schaal t.o.v. een nominale schaal is dat er een natuurlijke ordening bestaat tussen de categorieën. Dit wil zeggen er bestaat een soort hiërarchie tussen de verschillende categorieën. Daarnaast kan er in een ordinale schaal een nulpunt zijn gedefinieerd maar dit is een willekeurig nulpunt. Nul betekent hier dus niet de afwezigheid van het gene dat wordt gemeten. Dit houdt in dat eventueel negatieve waarden mogelijk zijn en 0 is een relatief getal. Voorbeelden van een ordinale schaal zijn onder andere een Likert-schaal, het academisch niveau (Bachelor, Master of Science, Doctor of Philosophy), Michelin sterren van een restaurant, een review schaal op Bol.com, Coolblue of Mediamarkt, en leeftijd indien gemeten in bandbreedtes (20-25 jaar, 26-30 jaar, 31-35 jaar, 36-40 jaar).
De eigenschappen van de ordinale schaal
De ordinale schaal bestaat uit categorieën met een bepaalde orde waarbij er geen betekenisvol nulpunt en is gedefinieerd. Daarnaast is de afstand tussen de categorieën niet gedefinieerd, en als gevolg is ook de afstand tussen de schaaldelen (lineariteit) van de schaal niet gedefinieerd. De rangtelwoorden ofwel rangnummers die de categorieën van een ordinale schaal krijgen geven daarom alleen de rangorde van de categorie aan en hebben geen aanvullende betekenis. Daarom is het bepalen van een gemiddelde en standaarddeviatie van een ordinale schaal onlogisch. Het midden van de distributie (verdeling) wordt daarom gemeten via de mediaan (median) en de spreiding van de distributie via de interkwartielafstand (interquartile range (IQR)).
Kwantitatieve variabele:
Kwantitatieve variabelen zijn variabelen die zijn gebaseerd op een getalswaarde, denk hierbij onder andere aan temperatuur, leeftijd, lengte of bijvoorbeeld het aantal voorbijrijdende auto’s.
Discrete kwantitatieve variabelen
Discrete kwantitatieve variabelen zijn variabelen die losse waarden aannemen. Tussenliggende waarden zijn niet gedefinieerd en hebben dus geen waarde. Bijvoorbeeld een telvariabele is een discrete variabele. Je kan het aantal auto’s tellen dat voorbijrijdt, maar je kan alleen hele auto’s tellen. Kortom, een discrete kwantitatieve variabele is niet deelbaar.
Continue kwantitatieve variabelen
Een continue kwantitatieve variabele is gebaseerd op aaneengesloten oneindig aantal deelbare eenheden. Enkele voorbeelden van continu kwantitatieve variabelen zijn lichaamslengte, gewicht, snelheid en temperatuur.
Continue schaal (continuous)
Intervalschaal
Een interval schaal heeft veel overeenkomsten met een ordinale schaal, het is een geordende schaal waarbij er een natuurlijke ordening (hiërarchie) is tussen de categorieën. Het bijzondere aan de interval schaal t.o.v. de ordinale schaal is dat de afstand tussen de categorieën/ schaaldelen is gedefinieerd en gelijk is. Dit wil bijvoorbeeld zeggen dat de afstand tussen 1 en 2 is hetzelfde als de afstand tussen 5 en 6. Daarnaast kan in deze schaal ook een nulpunt gedefinieerd zijn maar dit is een willekeurig nulpunt. Nul betekent hier dus niet de afwezigheid van het gene dat wordt gemeten. Dit houdt in dat eventueel negatieve waarden mogelijk zijn en nul is een reel getal. Een voorbeeld van een intervalschaal is onder andere de temperatuur in graden Celsius. De temperatuurschaal in Celsius heeft een vaste schaalafstand en een hiërarchie, maar het nulpunt is willekeurig.
Waarom kan je variabelen op een interval schaal niet delen of vermenigvuldigen?
Voor het delen of vermenigvuldigen van twee getallen is het belangrijk dat deze getallen beide een absoluut (betekenisvol) nulpunt hebben. Een ratio (deling) van twee getallen heeft alleen betekenis als beide getallen kunnen relateren aan een nulpunt. Een veel gebruikt voorbeeld om de noodzaak van een gemeenschappelijk (absoluut) nulpunt duidelijk te maken is de verschillen tussen de Celsius en Fahrenheit temperatuurschalen.
Hoe is het nulpunt van de Celsius en Fahrenheit temperatuurschalen bepaald?
Het nulpunt van de Celsius schaal is gemeten bij smeltend ijs en definieert als 0 graden. Hoe de Celsius temperatuurschaal verder is opgebouwd kan je hier lezen. Het nulpunt van de Fahrenheitschaal is gebaseerd op het bevriezen van zoutwater, hierdoor werd een lager temperatuur verkregen. Hoe de Fahrenheit temperatuurschaal verder is opgebouwd kan je hier lezen. Beide schalen zijn lineair maar hebben een ander nulpunt.
Een verdubbeling van het verschil betekend niet een verdubbeling van hetgeen dat wordt gemeten!
Doordat de nulpunten van de Celsius en Fahrenheit temperatuurschalen bepaald zijn op een arbitrair bepaald punt, betekent dat niet dat als de schaal nul bereikt dat er geen temperatuur meer is. Als de temperatuur van 20 naar 40 graden Celsius stijgt betekent dat niet dat er 2x zoveel temperatuur is. Het verschil ten opzichte van 0 graden Celsius is weliswaar verdubbeld maar niet de temperatuur. Hetgeen wat hier van belang is, is het referentieniveau. Als je 20 graden Celsius vergelijken met -10 graden Celsius dan is het verschil 30 graden. Als je dan over een verdubbeling van de temperatuur zouden willen praten dan zouden we 20 graden met 50 graden Celsius moeten vergelijken. Hier komt naar voren dat het referentieniveau bepalend is of een meeteenheid verdubbelt of halveert. Daarom is het delen of vermenigvuldigen van schalen zonder absoluut nulpunt betekenisloos.
De eigenschappen van de intervalschaal
Doordat de intervalschaal een vaste en gedefinieerde (equidistant) schaalafstand heeft, is het bepalen van een rekenkundig gemiddelde en standaarddeviatie van een interval schaal mogelijk. Een voorwaarde voor het bepalen van het rekenkundig gemiddelde is dat de variabele normaal verdeeld is. Als de variabele niet normaal verdeeld is (skewed), dan is een mediaan meer van toepassing. Daarnaast kan je met een intervalschaal rekenkundige bewerkingen worden gedaan zoals getallen optellen, aftrekken maar vermenigvuldigen en delen is niet mogelijk. Voorgaande roept dan gelijk de volgende vraag op.
Waarom kan ik wel een gemiddelde bepalen van een intervalschaal maar niet een delen of vermenigvuldigen?
De voornaamste reden is het ontbreken van een absoluut (niet willekeurig) nulpunt, hierdoor is de interpretatie van een deling of vermenigvuldiging discutabel. Een bijkomende reden is dat een deling (ratio) een andere bewerking is dan een het bepalen van een gemiddelde. Een gemiddelde is het meest voorkomende, typerende, getal in een variabele (getallenreeks) dat het midden van de verdeling aangeeft. Daarentegen is een deling (ratio) de verhouding van een getal (variabele) ten opzichte van een ander getal (andere variabele). Kortom, bij de berekening van een gemiddelde blijf je dus binnen dezelfde variabele, bij een deling (ratio) vergelijk je twee verschillende variabelen. Doordat je bij een deling (ratio) twee verschillende variabelen met elkaar vergelijk wordt het referentieniveau (nulpunt) relevant.
Geïnteresseerd in onze andere Tips? >>
Ratio schaal
Een ratioschaal heeft veel overeenkomsten met een interval schaal, hiermee bedoelen we dat het een geordende schaal heeft waarbij er natuurlijke ordening (hiërarchie) is tussen de categorieën en het een constante schaalafstand heeft. Het bijzondere aan de ratio schaal t.o.v. de interval schaal is dat er een absoluut (betekenisvol) nulpunt is gedefinieerd. Nul betekent hier dus de afwezigheid van het gene dat wordt gemeten. Dit houdt in dat nul niet bestaat en dat er geen negatieve waarde mogelijk zijn. Kortom, het nulpunt is een betekenisvolle inhoud. Een voorbeeld van een ratioschaal is onder andere de temperatuur in graden Kelvin. De temperatuurschaal in Kelvin heeft een vaste schaalafstand en een hiërarchie en het heeft een absoluut nulpunt. Andere voorbeelden van een ratioschaal zijn lengte en gewicht.
De eigenschappen van de ratio schaal
Doordat de ratio schaal een vaste en gedefinieerde schaalafstand heeft, is het bepalen van een gemiddelde en standaarddeviatie van een intervalschaal mogelijk. Daarnaast kunnen met deze schaal andere rekenkundige bewerkingen worden gedaan zoals getallen optellen, aftrekken, vermenigvuldigen en delen.
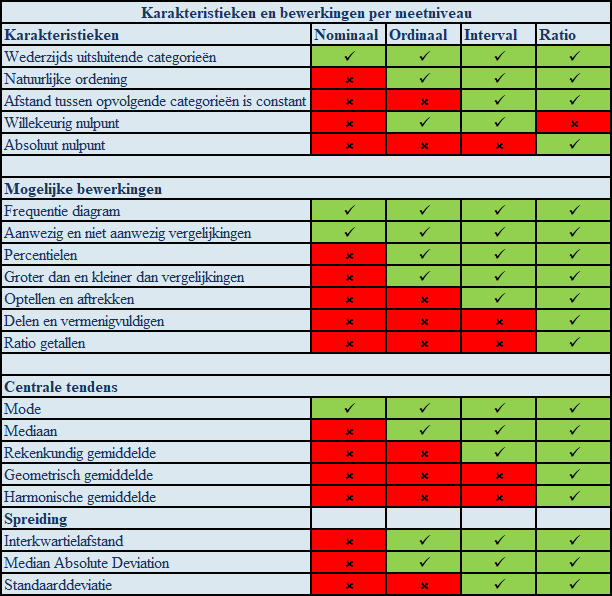
In onderstaande tabel zie je de karakteristieken en mogelijke bewerkingen bij de verschillende meetniveaus.