Missende waarden (missing values), en wat nu?

Je hebt net je data verzameld voor je scriptie of beroepsopdracht, misschien zelfs wel van meerdere bronnen, het was al een hele puzzel om die verschillende datasets samen te voegen en nu wordt het tijd om je dataset te inspecteren. Tot je teleurstelling kom je erachter dat je een groot aantal missende waarden (missing values) hebt. En als je een eerste regressie doet in SPSS of Stata blijft er maar een klein deel van je observaties over. Kortom, een zware teleurstelling. Je zit met je handen in het haar, wat moet je nu doen! Nog meer data verzamelen, weer een enquête de deur uit sturen? Grofweg zou je volgende negen opties kunnen overwegen.

De voorbereiding: Het bepalen wat de karakteristieken zijn van de missende data.

Voordat we de opties kunnen bespreken is het belangrijk om de karakteristieken (de aard) van de missende data te onderzoeken. Afhankelijk van deze karakteristieken zullen sommige opties geschikter zijn dan andere. Dit heeft te maken met de aannames en rekenmethode waar de onderstaande opties op gebaseerd zijn. Daarom, voordat je begint met het oplossen van de missende data is het handig eerst even in kaart te brengen wat de karakteristieken zijn van de missende data.

Drie verschillende karakteristieken (vormen) van missende data

Er zijn drie verschillende vormen waarin de missende data kan voorkomen, de drie vormen zijn als volgt (Little, 1988; Schafer & Graham, 2002).

1. Missing Completely at Random (MCAR)
2. Missing at Random (MAR)
3. Missing Not at Random (MNAR) / Not Missing at Random (NMAR)

Waarom onderscheid maken tussen de verschillende vormen van missende waarden?

Een variabele met MAR karakteristiek wordt ook wel geclassificeerd als “ignorable nonresponse” en een variabele met een MNAR-karakteristiek wordt ook wel geclassificeerd als “nonignorable nonrespons” (Little, 1982; Little & Rubin, 1989; Rubin, 1976; Schafer & Graham, 2002). Daarbij kunnen we ook onderscheid maken tussen respondenten die helemaal niet gereageerd hebben op de enquête (unit nonresponse / non response bias) en respondenten die niet hebben geantwoord op een of meerdere vragen (item nonresponse).

Ignorable nonresponse

Een “ignorable nonresponse” is een situatie waarbij het hele bereik van mogelijke waarden van de alle variabelen zijn vertegenwoordigd. Dit impliceert dat er geen structurele missende waarden zijn van een deel van de doelgroep. We kunnen dan met minder complexe methodes schatten wat de waarde had kunnen zijn en aan de hand van de bekende variabelen kunnen we de response van de afhankelijke variabele modeleren. Bijvoorbeeld doormiddel van een Maximum Liklihood schatting (ML), regressieanalyse, Multiple Imputation (MI) of Multiple Imputation by Chained Equations (MICE). De term, “ignorable nonresponse”, kan daardoor wel verkeerd worden geïnterpreteerd waarbij je de indruk krijgt dat je niets hoeft te corrigeren. De term “ignorable nonresponse” houdt uiteindelijk in dat de sample distributie van waarden een goede afspiegeling is van de distributie van alle mogelijke waarden (totale populatie) (Little, 1982).

Nonignorable nonresponse

Een “nonignorable nonresponse” is een situatie waarbij er systematisch waarden van de variabelen missen. Stel dat je de respondenten een vraag stelt over een gevoelig onderwerp, zoals salaris, religie, politieke voorkeur, …etc. Dan kunnen sommige respondenten besluiten de enquête niet (helemaal) in te vullen. Dan missen we dus structureel informatie van die groep respondenten. In het verlengde van wat we bij “ignorable nonresponse“ hebben besproken, is nu de distributie van waarde van de sample niet meer representatief voor de totale populatie (Little, 1982). We kunnen dan niet meer de voorgaande methoden gebruiken omdat we geen informatie hebben over een deel van de populatie. Op dat moment moeten we speciale schattingstechnieken gebruiken, zoals een Heckman regressie, om via een theoretisch model de waarde van de afhankelijke variabele te voorspellen. Het nadeel van deze methode(s) is dat het lastig is om aan de aannames van die test te voldoen.

Gratis Intakegesprek? >>

Missing at Random (MAR)

Als de kans dat een observatie mist voorspeld kan worden met behulp van de andere variabelen in de dataset en niet afhankelijk is van variabelen die niet in de dataset zitten dan beschouwen we dat de missende waarden willekeurig ontbreken. Hier bovenop is in de MAR-conditie de waarde van de missende variabele onafhankelijk van het feit of deze mist (Schafer & Graham, 2002). Hieruit blijkt dus dat we de missende observatie en zijn waarde kunnen voorspellen met behulp van de variabelen die aanwezig zijn in de dataset. Als we dit doen, dat zouden we dus het missen van desbetreffende waarde perfect moeten kunnen voorspellen zonder dat er nog een onverklaard gedeelte blijft (Schafer & Graham, 2002). Als er een onverklaard gedeelte achterblijft betekend dat dus dat er externe variabelen zijn die invloed uitoefenen op het ontbreken van de waarden.

Missing Completely at Random (MCAR)

De MCAR conditie word door Schafer and Graham (2002) gezien als een speciale conditie van de MAR karakteristieken. In de MCAR-situatie zijn de missende observaties zowel onafhankelijk van de variabelen die niet zijn opgenomen in de dataset als van de variabelen die wel zijn opgenomen in de dataset. Hier bovenop is in de MCAR-conditie de waarde van de missende variabele onafhankelijk van het feit of deze mist (Allison, 2000; Schafer & Graham, 2002).

MCAR-voorbeeld 1:

Als voorbeeld, stel dat je schriftelijk enquêteresultaten aan het verzamelen bent, en toevallig mors je koffie op een deel van je enquête bij de verwerking. Als resultaat is een of twee antwoorden van een respondent onleesbaar geworden. Het missen van deze observaties heeft niets te maken met de andere variabelen in je enquête of eventueel onbekenden variabelen. Daarnaast heeft het ontbreken van deze observaties dan ook niets te maken met de waarde van de observatie.

MCAR-voorbeeld 2:

Patrician (2002) geeft een ander illustratief voorbeeld. Stel, je hebt een enquête uitgevoerd en in een van de vragen vraag je of de respondent zijn gewicht wil invullen. Een aantal respondenten slaan deze vraag over maar vullen wel de rest van je enquête in. Je kan argumenteren dat vrouwen gevoeliger zijn m.b.t. dit onderwerp dan mannen. Daarnaast, kan je beargumenteren dat iemand met ondergewicht of iemand met overgewicht de vraag confronterend vindt of zich schaamt voor zijn/haar gewicht. Als je kan uitsluiten dan het feit dat de waarde mist niet te maken heeft met bijvoorbeeld het geslacht of het gewicht van die persoon dan zou je kunnen beargumenteren dat de missende waarden MCAR zijn. Of vrouwen systematisch deze vraag niet beantwoorden is eenvoudig te testen met de Little test R. J. A. Little (1988). Maar, of respondenten met onder- of overgewicht deze vraag niet beantwoorden is vaak niet te bepalen.

Wat kost scriptiebegeleiding? >>

Little test om te kijken of de missende waarde MCAR of MAR zijn.

1. Little (1988) heeft hiervoor een eenvoudige test bedacht. Creëer een dichotome, binaire variabele (dummy) die de waarde 1 krijgt als een observatie mist en de waarde 0 krijgt als de waarde niet mist. Vervolgens kan je via een t-tests of een chi-square test controleren of ver tussen deze variabele en de andere variabelen in de dataset een significant verschil zit. In Stata kan je eenvoudig de Little test doen via het mcartest commando (Li, 2013).

Missing Not at Random (MNAR)

De MNAR-conditie ontstaat wanneer er een het ontbreken van de waarde afhankelijk is van de waarde van die observatie (Allison, 2000; Schafer & Graham, 2002).  MAW de hoogte, het niveau of de categorie van die waarde bepaald of de waarde ontbreekt. Het probleem van MNAR is dat de sample niet meer een representatieve afspiegeling is van de totale populatie. Met ander woorden, jouw enquête responses (data) weerspielen de antwoorden van een specifiek deel van de totale doelgroep en niet meer de hele doelgroep. Op dat moment kunnen we niet meer met een kansberekening (probability sampling) schatten welke waarde de missende waarde zou moeten hebben (Little, 1982). In de MNAR-conditie moeten we de missende waarde voorspellen op basis van een model uit de literatuur waarbij we de aanname doen dat dat model op onze dataset van toepassing is.

Waarom kan een missende waardeafhankelijke zijn van zijn waarde?

Respondenten kunnen weigeren om antwoord te geven als je hun om gevoelige gegevens vraagt. Acock (2005) beargumenteert het heel mooi, stel dat je een telefonische enquête uitvoert naar de inkomens van de respondenten. Stel dat je Bill Gates aan de telefoon hebt en hem vraagt naar zijn inkomen, zal hij jou dan antwoord geven op die vraag? Een vergelijkbaar verhaal kan je bedenken voor respondenten met een zeer laag inkomen of uitkering. Zullen die jouw vraag over het inkomen willen beantwoorden? Als dit het geval is voldoet je niet aan de MCAR of MAR aannames.

Achterhalen of de missende waarde MNAR zijn.

Het probleem met Missing Not at Random (MNAR) observaties is dat we geen manier hebben om dat te bepalen. De “unknown unknowns” zijn namelijk niet te bepalen. In theorie zou de enige mogelijkheid zijn als je bijvoorbeeld een enquête hebt uitgevoerd, contact op te nemen met de respondenten die een vraag niet hebben beantwoord en proberen te achterhalen waarom zij de vraag niet willen beantwoorden. Het kan zelf nog uitgebreider, dan benader je de respondenten die de vragenlijst helemaal niet hebben ingevuld en vraagt hun een aantal van je belangrijkste vragen uit je enquête. Als hun antwoorden afwijken van de antwoorden van de respondenten die wel de vragenlijst hebben ingevuld dan is het feit dat een waarde mist waarschijnlijk MNAR. Vaak hebben we niet de luxe om dit te doen, enerzijds omdat de responses misschien anoniem zijn of omdat we geen idee hebben wie de non-responders zijn.

Waarom is MNAR een probleem?

Het verschil tussen MAR en MNAR is dat we in de MAR conditie willekeurige missende data hebben, dus het hele spectrum aan waarden is aanwezig alleen missen op willekeurige plaatsen waarden. Hierdoor kunnen we door diverse technieken heel goed schatten wat deze missende waarde zou moeten zijn. MNAR is een probleem omdat we dan een statistisch model moeten maken, zonder dat we data hebben om dat statistische model vorm te geven, die de missende waarde voorspeld. Kortom, we moeten een voorspelling doen wat die missende waarde zou moeten zijn als deze wel bekend zou zijn.  Dit zorgt ervoor dat we een grote foutmarge en miswijzing kunnen creëren met onze voorspelling.

Een MNAR-voorbeeld:

Stel dat je de salarissen van bepaalde groep wil meten, om dat te doen stuur je een enquête rond aan bijvoorbeeld 500 managers. Maar, het salaris dan iemand krijgt is vaak een gevoelig onderwerp. Stel nu dan managers die minder dan $2000 dollar per maand verdienen zich een beetje schamen en die vraag in je enquête niet willen invullen, of sterker nog als ze die vraag zien je enquête helemaal niet willen invullen, of door jouw instelling dat deze vraag verplicht moet worden ingevuld zij stoppen met de enquête. Een vergelijkbare redenatie kan je bijvoorbeeld hebben bij managers die meer dan $7000 per maand verdienen, zij kunnen ook terughoudend zijn met het geven van deze informatie. Kortom, als je een deel dat de enquête wilde invullen teruggekregen hebt mis je dus de antwoorden van managers die minder dan $2000 en meer dan $7000 verdienen.

De analyse van de MNAR-enquête responses.

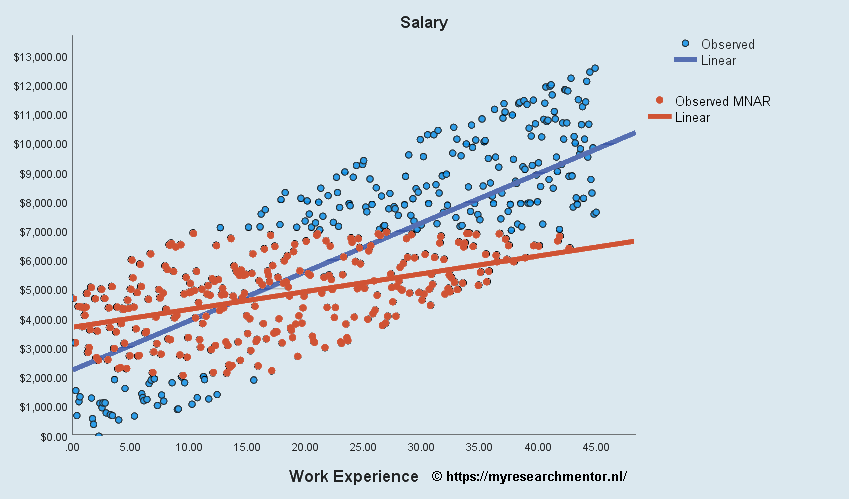
Doordat je nu op structurele basis bepaalde groepen responses mist komt je regressieanalyse niet met het correcte resultaat terug. In onderstaande figuur is te zien dat als je de responses van lager dan $2000 en hoger dan $7000 niet meeneemt in je analyse de regressielijn opmerkelijk vlakker loopt. Hierdoor is er dus een miswijzing (bias) ontstaan. Afhankelijk van de ernst van de missende waarden, kan niet alleen de steilheid van de regressielijn worden beïnvloed maar in sommige gevallen ook of deze positief of negatief is. Hierdoor, is MNAR (oranje datapunten) een problematische situatie.

 

Neem contact met mij op! >>

Zijn er oplossingen voor een MNAR-conditie?

Het is natuurlijk een beetje flauw om te zeggen, maar ja, de eerste oplossing is te onderzoeken wat de oorzaak is van de MNAR-conditie en of er een verschil is met de bekende observaties. Alleen is dit in sommige gevallen niet mogelijk. Een bekende regressie techniek om rekening te houden met MNAR-observaties is bijvoorbeeld een Heckman-regressie. Deze Heckman-regressie corrigeert voor de missende waarde door aan de hand van een Probit-regressie (binaire regressie) op het wel of niet aanwezig zijn van afhankelijke variabele een voorspelling te doen wat de correctie is die moet worden meegenomen in de OLS-regressie (Inverse Mills Ratio). Zie onder andere de volgende voorlichtingsvideo. Hieruit wordt ook duidelijk dat het belangrijk is om te controleren of je aan de aannames van de Heckman test voldoet. Als je niet aan deze aannames voldoet is het in sommige gevallen beter om terug te vallen op de MAR technieken.

Optie 1: Het aanvullen van de missende data.

Alhoewel dit in veel (scriptie / beroepsopdracht) onderzoeken niet of niet eenvoudig is heeft het de voorkeur om een poging te wagen om alsnog de missende data te kunnen verkrijgen. De andere opties die hieronder staan vermeld zijn een benadering, een schatting, van de werkelijkheid. Met die schatting(en) introduceer je een veronderstelling, een aanname, van de werkelijkheid wat een miswijzing (bias) kan opleveren en een beperking is van de onzekerheid (variatie).

Survey based research

Bijvoorbeeld door de respondent nogmaals te benaderen en vragen waarom hij/zij de vraag niet heeft ingevuld. Dat kan natuurlijk alleen als je enquête niet anoniem is en je de respondent kent en kan benaderen. Het kan zijn dat de vraagstelling of de antwoordschalen hier een oorzaak van waren. Daarom, is het altijd verstandig je enquête eerst onder een testgroep (pilot) uit te zetten om dit soort zaken vroegtijdig te ontdekken. Een andere reden kan zijn dat de (stakeholder)groep waar de respondent toe behoord maar beperkte antwoorden kan geven op de vragen. Dit zou misschien kunnen duiden op dat je de verkeerde (stakeholder)groep hebt benaderd met je vragen. Dan, is het je samplingstrategie heroverwegen en opnieuw je enquête uitzetten onder een beter passende (stakeholder)groep.

Second source based research

Als je je onderzoek baseert op second source data kan het, verglijkbaar als hierboven, je een categorie data hebt verzameld die niet bij je onderzoeksopzet past. Bijvoorbeeld, als Research and Development (R&D) een belangrijk onderdeel is van je onderzoek, en je onderzoekt de textiel- of meubelindustrie, dan zal je weinig bedrijven aantreffen die R&D uitgave rapporteren.  Als je ervan overtuigd bent dat je de correcte doelgroep te pakken hebt, dan kan je kijken of je de missende data nog via alternatieve bronnen kan verkrijgen, bijvoorbeeld andere databanken, de jaarverslagen op de website van het bedrijf of die zijn ingeleverd bij een officiële instantie zoals een beurs, …etc.

Kortom in beide bovenstaande gevallen zou je kunnen concluderen dat er een positioneringsvergissing is gemaakt in de onderzoeksopzet. Hier is vaak weinig aan te doen anders dan het analyseren van de onderzoekopzet en het onderzoek opnieuw uitvoeren bij een beter passende doelgroep.

Optie 2: De missende data alsnog aanvullen met andere databronnen

Stel dat je demografische gegevens bent vergeten te vragen aan de respondent. Dan zou je via sociale mediawebsites zoals LinkedIn nog achter een beperkt aantal zaken kunnen komen. Zorg er dan wel voor dat heel duidelijk is in je scriptie (beroepsopdracht) waar welke data vandaan komt. Daarnaast onderbouw dat de bronnen die je gebruikt betrouwbaar en valide zijn. Als je financiële data van bedrijven verzameld, zou je bijvoorbeeld via de jaarverslagen op de websites of op de websites van beurzen zoals de Securities and Exchange Commission (SEC) kunnen opvragen en de missende data opzoeken. In beide voorgaande gevallen, zorg ervoor dat je “bewijsmateriaal” veilig opslaat op je eigen computer. Een document op een website kan namelijk altijd worden veranderd of verwijderd!

Optie 3: Een complete case analysis (Listwise deletion)

Je kan besluiten dat missende data is simpelweg missende data. De desbetreffende variabele voor die case laat je dan leeg. Dan accepteer je een miswijzing (bias) in je resultaten. Je zal dan heel nauwkeurig je sample group moeten omschrijven om duidelijk de maken dat deze resultaten alleen gelden voor deze groep.

Wanneer zou je een complete case analysis kunnen overwegen?

Een respondent op een grote groep zal waarschijnlijk je resultaat niet veel veranderen, maar als dit meerdere respondenten betreft kom je voor een methodologische en ethische keus te staan. De vuistregel in de literatuur is dat al de missende waarde minder dan 10% van de observaties zijn een complete case analysis acceptabel is. Tsikriktsis (2005) adviseert om complete case analysis niet toe te passen omdat dit het statistisch detectievermogen (power) reduceert.

De mitsen en maren van een complete case analysis

Je kan een complete case analysis overwegen als je ervan bent overtuigd dat alle andere methoden incorrect zijn. Acock (2005) geeft aan dat een complete case analysis alleen acceptabel is als de missende waarden een MCAR-karakteristiek hebben en de dataset van voldoende omvang is. Maar,  Acock (2005) geeft ook aan dat de MCAR aanname vaak onredelijk en onrealistisch is. Hieruit blijkt al, er is geen gemakkelijk antwoord op missende waarden. Indien, de waarden die missen willekeurig missen, dan zou je een regressie kunnen overwegen waarbij de missende cases worden verwijderd. Maar, als de missende waarden niet willekeurig missen (Missing not at Random (MNAR)), zou een complete case analysis tot een lagere statistisch power en miswijzing (Bias) kunnen leiden. Als gevolg is een van de andere methoden dan noodzakelijk.

Optie 4: Een Ridge of Lasso regressie

Als je een kleine dataset hebt van +/- 100 observaties zou je kunnen overstappen op een ridge of lasso regressie. Deze regressie technieken kunnen tot een beter resultaat leiden als je aanzienlijke multicollineariteit hebt of als je meer variabelen dan observaties hebt. Het nadeel van deze technieken is dat de variantie wordt verminderd ten koste van de bias (Nischal, 2019). Dit wil zeggen, dat er een miswijzing van de regressie coëfficiënt wordt geaccepteerd om daarmee de standaard error te verkleinen. Als het doel van het onderzoek is om de bias zo klein mogelijk te houden kan je overwegen om andere technieken te gebruiken.

Optie 5: Het vervangen van de Missende waarden door het gemiddelde (Mean imputation)

Het vervangen van de missende waarden door het gemiddelde is een veel gebruikte methode, maar die niet onomstreden is. Het vervangen van de missende data door het gemiddelde van de bekende data van een variabele neemt aan dat een willekeurige observatie kan worden uitgewisseld met de typische waarde van de groep. Als je goed nadenkt over de implicaties van die aanname zullen er wel wat vragen bij je opkomen?

Een voorbeeld van de nadelen van mean imputation.

Bijvoorbeeld, als je het missende antwoord van een respondent vervangt door het gemiddelde van de andere respondenten, neem je aan dat die respondent dat gezegd zou hebben. Maar, is dat wel zo? Acock (2005) beargumenteert het heel mooi, stel dat je een telefonische enquête uitvoert naar de inkomens van de respondenten. Stel dat je Bill Gates aan de telefoon hebt en hem vraagt naar zijn inkomen, zal hij jou dan antwoord geven op die vraag? Stel nu dat Bill Gates geen antwoord geeft en je vult daarvoor het gemiddelde antwoord van de andere respondenten in, is dat dan een goede aanname? Een vergelijkbaar verhaal kan je bedenken voor respondenten met een zeer laag inkomen of uitkering. Zullen die jouw vraag over het inkomen willen beantwoorden, of nog ernstiger, eerlijk willen beantwoorden? Als je dan ook die antwoorden door het gemiddelde antwoord vervangt, is dat dan een terechte en te rechtvaardigen aanname?

Wanneer wordt mean imputation een probleem?

Acock (2005)  geeft aan dat als het aantal missende waarde rond de 30% zit de het vervangen van de missende waarde door het gemiddelde een probleem kan gaan vormen. Dit betekent dan dat 30% van de data niet varieert. Dit is belangrijk als je van plan bent om een regressie of een ANOVA-analyse wil gaan doen, want deze analyse zijn een analyse van variantie. En “om iets te analyseren moet er wel iets variëren”. Daarnaast, kan het effect van de observaties waar je wel een “echte” waarde van hebt worden versterkt. Dit wil zeggen, hun afwijking t.o.v. van het gemiddelde telt zwaarder mee. De regressiecoëfficiënt zal daardoor meer en meer richting 0 bewegen, wat een miswijzing (bias) richting 0 inhoud (Donders, van der Heijden, Stijnen, & Moons, 2006). Daarentegen, een regressie is een conditionele analyse, dus de coëfficiënten zijn conditioneel op de variabelen opgenomen in het regressiemodel. Hierdoor zal de coëfficiënt, van de andere variabelen versterkt, overschat, worden. Tsikriktsis (2005) adviseert om mean imputation alleen toe te passen als er minder dan 10% van de observaties mist.

Het effect van Mean Imputation in een MNAR-conditie

In onderstaande figuur is aan de horizontale lijn van paarse datapunten te zien dat als de missende waarden door het gemiddelde worden vervangen de miswijzing van de regressielijn nog groter wordt dan in de MNAR-conditie. De regressielijn loopt bijna horizontaal. Daarom wordt doorgaans afgeraden om een de missende waarden te vervangen door een constante waarde zoals een gemiddelde of een 0.

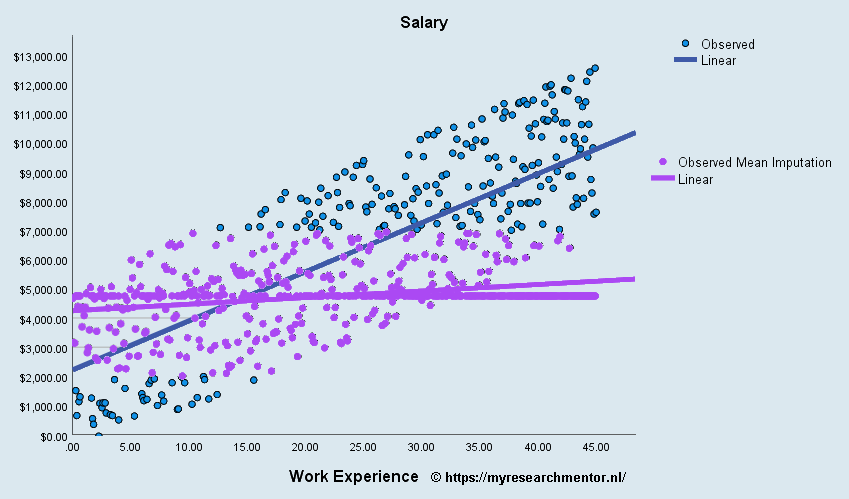
Een vergelijking van alle data, MNAR, en MNAR plus mean imputation

Een vergelijking van de effecten als je alle data zou hebben (blauw), MNAR waarden (rood) en als je in een MNAR conditie de missende waarde met gemiddelde waarden zou opvullen.

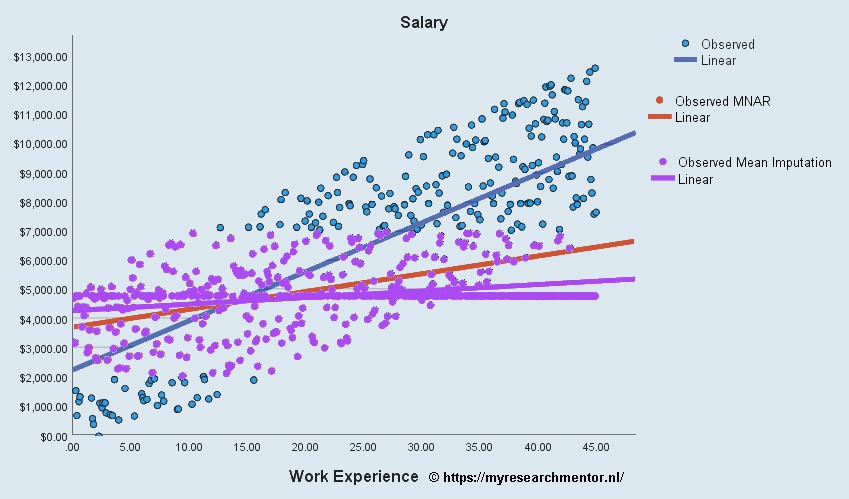
Het effect van Mean Imputation in een MAR-conditie

Hiervoor hebben we een extreme conditie laten zien, namelijk MNAR-conditie + mean imputation. Je zou kunnen arguementeren dat in de MAR-conditie mean imputation geen probleem is. Namenlijk de missende waarden ontbreken willlekeurig, het hele bereik van mogelijk datapunten zit in de database. De datapunten zijn een representatieve afspiegeling van de totale populatie. Daarbovenop zou je kunnen zeggen dat het toevoegen van een gemiddelde aan een gemiddelde geen effect heeft. Hier zou je gelijk in kunnen hebben als je alleen een beschrijvende analyse zou doen op basis van gemiddelden. In onderstaand voorbeeld laten we zien wat er gebeurt als je volkomen willekeurig 42% van de waarden weghaalt en vervangt door het gemiddelde. De blauwe datapunten en regressie lijn zijn de oorspronkelijke “volledige” dataset. De groene datapunten en regressielijn zijn van de dataset waarbij volkomen willekeurig 42% van de data is verwijderd en vervangen door het gemiddelde.

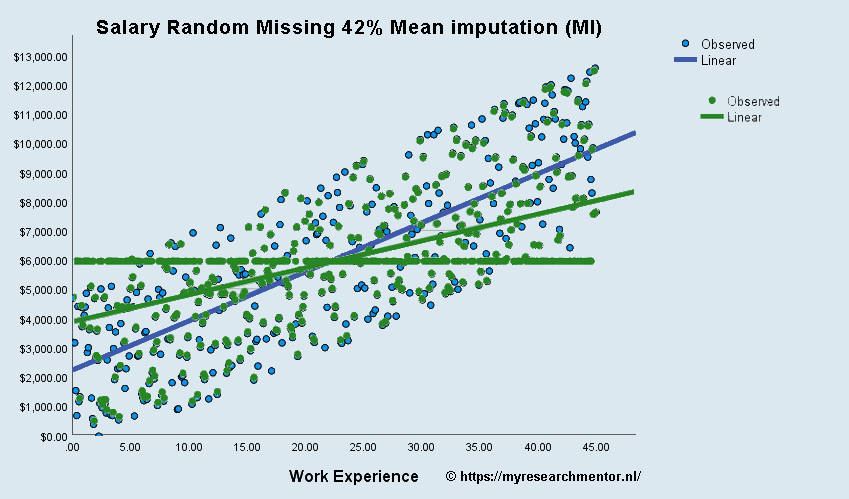
Conclusie MAR-conditie + Mean Imputation:

Je ziet een vergelijkbaar effect als bij de MNAR-conditie. Er is een merkbaar verschil in de helling van de regressielijn (slope), m.a.w. de beta coefficient van je regressie-analyse. Aangezien de hellingshoek van de regressielijn (slope) en de sterkte van van je beta coefficient (β) aan elkaar verbonden zijn, kan je beredeneren dan bij mean imputation de regressielijn dichter naar 0 naderd. Als dit in te sterke mate gebeurt zal op gegeven moment, afhankelijk van je betrouwbaarheids-interval, ook je regressie coefficient niet meer significant zijn.

Is alleen het vervangen van de missende waarde door het gemiddelde een probleem?

Het korte antwoord hierop is nee.  Alle constante waarden waarmee je de missende waarden vervangt kunnen een probleem vormen. Als je veel waarden vervangt door het gemiddelde gaat de variabele zich min of meer gedragen als een constante. Een vergelijkbaar verhaal gaat natuurlijk op als je de missende waarde vervangt door een 0 of elke andere waarde.

Het effect van Zero Imputation in een MNAR-conditie

In onderstaande figuur is aan de horizontale lijn van oranje datapunten te zien dat als de missende waarden door de waarde nul worden vervangen de miswijzing van de regressielijn nog groter wordt dan als we deze vervangen door het gemiddelde. Zowel de constante, de intercept, van de regressielijn als zijn hellingshoek (slope) zijn aanzienlijk anders dan in de volledige dataset (blauwe datapunten). Als je deze resultaten zou interpreten en rapporteren, in je conclusie zetten dat als mensen meer werkervaring hebben ze minder gaan verdienen. Dat zal dan een interessante discussie met je begeleider of examinatoren opleveren tijdens je verdediging. Daarom wordt doorgaans afgeraden om een de missende waarden te vervangen door een constante waarde zoals een gemiddelde of een 0.

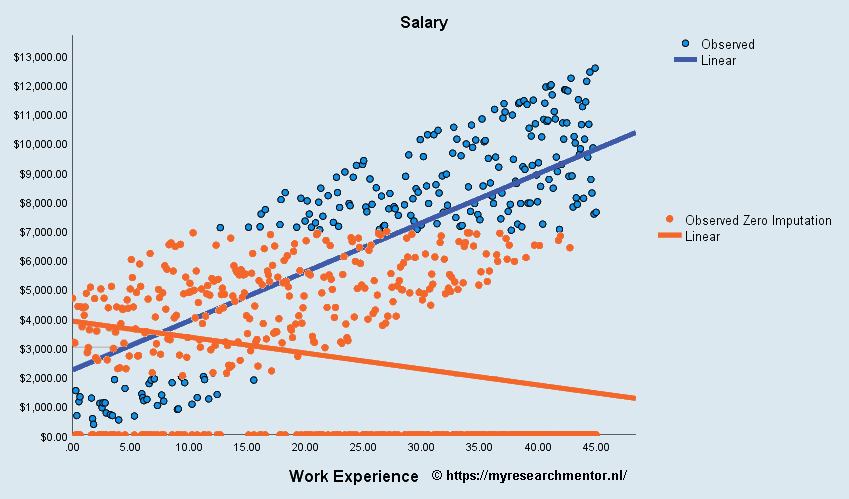
Het effect van Zero Imputation in een MAR-conditie

Hiervoor hebben we een extreme conditie laten zien, namelijk MNAR-conditie + zero imputation. Je zou kunnen arguementeren dat in de MAR-conditie zero imputation geen probleem is. Namenlijk de missende waarden ontbreken willlekeurig, het hele bereik van mogelijk datapunten zit in de database. Daarbovenop zou je kunnen zeggen dat de dataset een goede afspiegeling is van de totale populatie. Daarnaast zou je kunnen argumenteren dat als er geen waarde bekend is, deze waarschijnlijk gelijk aan nul is. Bijvoorbeeld, als er geen research and development (R&D) uitgaven worden gerapporteerd, dan is product-innovatie waarschijnlijk geen prioriteit voor het bedrijf.  In onderstaand voorbeeld laten we zien wat er gebeurt als je volkomen willekeurig 42% van de waarden weghaalt en vervangt door nul. De blauwe datapunten en regressie lijn zijn de oorspronkelijke “volledige” dataset. De oranje datapunten en regressielijn zijn van de dataset waarbij volkomen willekeurig 42% van de data is verwijderd en vervangen door nul.

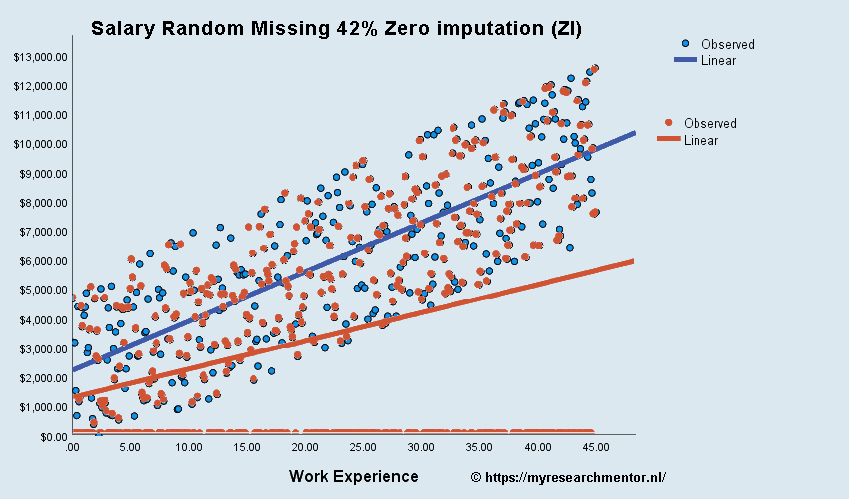
Conclusie MAR-conditie + Zero Imputation:

Je ziet een vergelijkbaar effect als bij de MNAR-conditie. Er is een merkbaar verschil in de helling van de regressielijn (slope), m.a.w. de beta coefficient van je regressie-analyse. Aangezien de hellingshoek van de regressielijn (slope) en de sterkte van van je beta coefficient (β) aan elkaar verbonden zijn, kan je beredeneren dan bij zero imputation de regressielijn dichter naar 0 naderd. Als dit in te sterke mate gebeurt zal op gegeven moment, afhankelijk van je betrouwbaarheids-interval, ook je regressie coefficient niet meer significant zijn. Daarnaast, zie je dat de intercept, de constante, waar de regressielijn begint lager is geworden. Kortom, het vervangen van missende waarden met nullen is zowel in de MNAR als in de MAR situatie onverstandig. Hier in een nadere analyse van de data verstandig, probeer te achterhalen waarom er data mist. Je kan bijvoorbeeld deels een verkeerde doelgroep in je analyse hebben opgenomen, een groep die niet bij je analyse past.

Variabele correctie door middel van een indicator / dummy variabele.

Een populaire methode is dan om gebruik te maken van de conditionele eigenschappen van de regressie en een indicator variabele (dummy) op te nemen in de regressie die de missende waarden van de niet missende waarden onderscheid (Cohen, West, & Aiken, 2003). Als deze methode wordt toegepast zijn de regressiecoëfficiënten gelijk aan de regressiecoëfficiënten bij een complete case analysis (listwise deletion), maar de standaard error van de regressiecoëfficiënt is lager dan hij zou moeten zijn als de missende observaties een daadwerkelijke waarde hadden.  Donders et al. (2006) en Acock (2005)  adviseren om dat niet te doen omdat dit zorgt in een miswijzing (bias) van je resultaten. Kortom, deze methode werkt, maar alleen als het aantal missende waarde beperkt is, bijvoorbeeld minder dan 30% (Shrive, Stuart, Quan, & Ghali, 2006). En dat deze methode alleen op enkele variabelen wordt toegepast. (Tsikriktsis, 2005)

Optie 6: Het voorspellen van de missende waarden met behulp van een regressieanalyse.

Je zou natuurlijk ook de waarde van de ontbrekende observaties kunnen voorspellen met een regressieanalyse. Daarvoor kan je op basis van de voorgaande literatuur bepalen welke variabelen belangrijke voorspellers zijn van de variabele die je wil berekenen. Er is dan min of meer als een nomologisch netwerk dat aangeeft waar de missende waarde van afhankelijk is.  De paper van Mits ga, Ramos, and Frias (2011) geeft bijvoorbeeld een voorbeeld van een nomologisch netwerk. Volgens Tsikriktsis (2005) word de regressie methode doorgaans gebruikt als er meer dan 20% missende waarden zijn.

Wat zijn de mitsen en maren van een voorspelde waarde op basis van een regressieanalyse?

Bij deze methode voer je eerst een regressieanalyse uit waarbij de variabele met missende waarde de afhankelijke variabele is en de variabelen uit je nomologisch netwerk de voorspellers zijn. Vervolgens laat je de regressieanalyse de voorspelde waarde berekenen (opslaan) van je afhankelijke variabelen. De missende waarden vervang je dan met deze voorspelde waarde.

De regressie methode levert weliswaar een voorspelde waarde van de missende waarde op die varieert afhankelijk van de onafhankelijke variabelen, maar wordt nog steeds bekritiseerd omdat hij onvoldoende rekening houdt met de variatie in de data (Acock, 2005; Donders et al., 2006; R. J. A. Little & Rubin, 1989). Een regressieanalyse schat namelijk maar 1 waarden voor het missende datapunt, reduceert daarmee de standaarddeviatie en neemt daarbij de onzekerheid van deze schatting niet mee.

Optie7: In panel data de waarde van de voorgaande observatie overnemen (LOCF).

Als je panel-data hebt, d.w.z. een herhaalde meting van hetzelfde object, dan wordt in enkele gevallen ook wel de “Last Observation Carried Forward” (LOCF) gebruikt (Kang, 2013; R. J. Little et al., 2012). Bij deze methode kijk je wat de laatst bekende waarde is van een bepaalde respondent en vervang je de missende waarde door de laatst bekenden waarde.

Een voorbeeld van LOCF:

Als je een bedrijf gedurende 10 jaar observeert en van de laatste 4 jaar heb je geen data, dan kijk je naar de observatie van jaar 6 en vul je deze observatie in jaar 7 t/m 10 in. Je kan je voorstellen dat deze methode ook tegen bezwaren aan loopt. Ten eerste, heb je dan de laatste jaren geen variatie in de data. Ten tweede, neem je aan dat de waarde de laatste jaren hetzelfde is als het laatste bekende jaar. Deze aannames zorgen dus wederom voor een miswijzing (bias) in je resultaten. Kang (2013) en R. J. Little et al. (2012) adviseren dan ook om deze methode niet te gebruiken tenzij je sterke onderbouwde statistische redenen hebt om dat te doen.

Optie 8: Maximum likelihood regressie

Schafer and Graham (2002) laten zien dat een Full Information Maximum Liklihood (FIML) regressie goed kan omgaan met missende waarden op voorwaarde dat deze Missing Completely at Random (MCAR) of Missing at Random (MAR) karakteristieken hebben. Data met Missing Not at Random (MNAR) karakteristieken, waarbij dus data systematisch mist, daar maakt de FILM regressie een schattingsfout.

Optie 9: Multiple Imputation (MI) & Multiple Imputation by Chained Equations (MICE)

Multiple Imputation (MI) en Multiple Imputation by Chained Equations (MICE) zijn verwante methodes die we hier gecombineerd besprekend. Beide methodes zijn gebaseerd op een MAR conditie aanname (Schafer & Graham, 2002). De voorkeur is natuurlijk altijd om alsnog achter de waarde van de missende observaties te komen. Als dat niet mogelijk is, is op dit moment in de tijd d volgens verschillende gerenommeerde auteurs en artikelen met veel invloed de MI- en MICE-techniek de methode van voorkeur. Een van de grondleggers van de MI-techniek is Rubin (1987) waarbij hij zich baseerde op het voorgaande onderzoek van (Allan & Wishart, 1930; Dempster, Laird, & Rubin, 1977; Yates, 1933). In het boek en op de website van Stef Van Buuren is een kort en bondig historisch overzicht gegeven (Van Buuren, 2018).

Hoe werkt de MI/MICE techniek?

Azur, Stuart, Frangakis, and Leaf (2011) hebben een zeer toegankelijk artikel geschreven waarin zij stap voor stap uitleggen hoe in essentie de MICE-techniek werkt.

Stap 1:

In de eerste stap (1) worden de missende waarden voor alle variabelen vervangen door een “placeholder”, bijvoorbeeld het gemiddelde. Nu zal je je afvragen op basis van de informatie hierboven of dat wel zo verstandig is. Daarom, is het belangrijk deze techniek in zijn geheel te bekijken.

Stap 2:

Vervolgens, wordt in de tweede stap (2) van een van de variabelen (bijvoorbeeld variabele x1) de “placeholders’ weer teruggezet naar missende waarden.

Stap 3:

Daarna, wordt in de derde stap (3) deze variabele x1 als afhankelijke variabele gebruikt en een of meerdere andere variabele in de dataset als onafhankelijke variabele.

Stap 4:

Hierop volgend laten we in stap vier (4) de regressie de voorspelde waarde berekenen conform het model dat we hebben gespecificeerd van variabele x1. Dus, als je maar enkele onafhankelijke variabelen hebt gespecificeerd in stap drie, zal je voorspelling niet erg nauwkeurig zijn. Daarom, is het verstandig een goed gespecificeerd model te gebruiken. De regressie berekend voor alle observaties, zowel de bekende als de missende waarden, een geschatte waarde. Vervolgens vervangen we in variabele x1 de missende waarde door de voorspelde waarde (imputations).

Stap 5:

Dit proces, stap 1 t/m 4, herhalen we voor alle variabelen welke missende waarden hebben. Als we alle variabelen hebben gehad, dan is er een cyclus afgerond.

Nu zal je waarschijnlijk wel denken, prima, maar dan zit nog steeds de fout van de mean imputation in alle variabelen. Daarnaast, deze procedure lijkt veel op de regressieanalyse in optie 6. Je zal je afvragen of we daarmee eigenlijk niet optie 5 en optie 6 hebben gecombineerd.

Stap 6:

De voorgaande stappen, stap 1 t/m 5 worden een aantal maal herhaald, doorgaans tussen 5 en 10 maal. Maar, meer herhalingen zijn mogelijk, het een en ander is voornamelijk afhankelijk van de sterkte van je processor, je opslagcapaciteit en het geheugen in je computer. Wulff and Ejlskov (2017) beargumenteren dat als je bijvoorbeeld 10 herhalingen doet de imputations stabiliseren. Met andere worden de gemiddelden en standaarddeviaties van elke herhaling wijken niet meer veel van elkaar af. De eerste 9 herhalingen worden dan als de “burn-in period” beschouwd.

Multiple Imputation by Chained Equations (MICE) in Stata en SPSS

Hieronder beschrijven we op hoofdlijnen hoe je een MICE-techniek zou kunnen toepassen in Stata of SPSS. Er zijn een aantal heel praktisch en toegankelijk geschreven artikelen die de MICE-techniek toelichten en uitleggen. Als je hier op in wil lezen zijn de artikelen van Wulff and Ejlskov (2017) en Azur et al. (2011) de moeite waard om eens door te lezen.

De implementatie van Missing Value Analysis (MVA) in SPSS

De Missing Value Analysis (MVA) module in SPSS was tot versie 17 van SPSS een add-on die los bij SPSS moest worden aangeschaft. Sinds versie 17 van SPSS is de MVA-module een onderdeel geworden van het basispakket. Deze toevoeging is een positieve ontwikkeling, maar de implementatie van de MVA-module is iet onomstreden. von Hippel (2004) heeft de MVA-module van SPSS geanalyseerd en is kritisch op de mogelijkheden die deze module biedt maar ook dat deze module de onzekerheid van de schatting van de missende waarde niet meeneemt. Als deze onzekerheid van de schatting niet wordt meegenomen wordt er alsnog een miswijzing (bias) gecreëerd (Acock, 2005; Graham, 2009). Een interesante instructie hoe je MVA in SPSS kan doen vind je onder andere in de workshop van Braitman (2016).

De implementatie van Missing Value Analysis (MVA) in Stata

De Multiple Imputation (MI) of Multiple Imputation by Chained Equations (MICE) in Stata zijn wat uitgebreider dan in SPSS, en je moet dat dat betreft wat meer instellen.  Aangezien de procedure in Stata veel stapjes en beslismomenten heeft, en we lengte van deze webpagina beperkt willen houden, adviseren we je om onderstaande bronnen aandacht door te nemen, en te experimenteren met een kleine dataset.

De “multiple imputation in Stata” pagina van de Universiteit van Californië – Los Angeles (UCLA) laat stap voor stap zien wat je in Stata moet doen als je de missende waarde via een “multiple imputation” methode wil verminderen. De Stata conferentiepresentatie van Marchenko (2011) geeft additioneel inzicht hoe je in Stata een MICE analyse kan uitvoeren. Als je hele gedetailleerde informatie zoekt over “multiple imputation” kan je natuurlijk altijd even de Stata multiple-imputation manual raadplegen.

Geïnteresseerd in onze andere Tips? >>

Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.

Contact! >>     WhatsApp Ons! >>

Ben je benieuwd wat onze scriptiebegeleiding (scriptiehulp) je kost? Neem dan een kijkje op onze tarievenpagina via onderstaande button!

Wat kost scriptiebegeleiding? >>

Literatuurlijst:

1. Acock, A. C. (2005). Working With Missing Values. Journal of Marriage and Family, 67(4), 1012-1028. doi:10.1111/j.1741-3737.2005.00191.x
2. Allan, F. E., & Wishart, J. (1930). A Method of Estimating the Yield of a Missing Plot in Field Experimental Work. The Journal of Agricultural Science, 20(3), 399-406. doi:10.1017/S0021859600006912
3. Allison, P. D. (2000). Multiple Imputation for Missing Data:A Cautionary Tale. Sociological Methods & Research, 28(3), 301-309. doi:10.1177/0049124100028003003
4. Azur, M. J., Stuart, E. A., Frangakis, C., & Leaf, P. J. (2011). Multiple imputation by chained equations: what is it and how does it work? International journal of methods in psychiatric research, 20(1), 40-49. doi:10.1002/mpr
5. Braitman, A. L. (2016). Data Cleaning Workshop: How to Prepare your Data Prior to Analysis. Retrieved from https://fs.wp.odu.edu/abraitma/wp-content/uploads/sites/1682/2016/05/Data-Cleaning-Workshop_color.pdf
6. Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3 ed.). New York: Routledge.
7. Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum Likelihood from Incomplete Data Via the EM Algorithm. Journal of the Royal Statistical Society: Series B (Methodological), 39(1), 1-22. doi:10.1111/j.2517-6161.1977.tb01600.x
8. Donders, A. R. T., van der Heijden, G. J. M. G., Stijnen, T., & Moons, K. G. M. (2006). Review: A gentle introduction to imputation of missing values. Journal of Clinical Epidemiology, 59(10), 1087-1091. doi:10.1016/j.jclinepi.2006.01.014
9. Graham, J. W. (2009). Missing Data Analysis: Making It Work in the Real World. Annual Review of Psychology, 60(1), 549-576. doi:10.1146/annurev.psych.58.110405.085530
10. Kang, H. (2013). The prevention and handling of the missing data. Korean journal of anesthesiology, 64(5), 402-406. doi:10.4097/kjae.2013.64.5.402
11. Li, C. (2013). Little’s Test of Missing Completely at Random. The Stata Journal, 13(4), 795-809. doi:10.1177/1536867×1301300407
12. Little, R. J., D’Agostino, R., Cohen, M. L., Dickersin, K., Emerson, S. S., Farrar, J. T., . . . Stern, H. (2012). The Prevention and Treatment of Missing Data in Clinical Trials. New England Journal of Medicine, 367(14), 1355-1360. doi:10.1056/NEJMsr1203730
13. Little, R. J. A. (1982). Models for Nonresponse in Sample Surveys. Journal of the American Statistical Association, 77(378), 237-250. doi:10.1080/01621459.1982.10477792
14. Little, R. J. A. (1988). A Test of Missing Completely at Random for Multivariate Data with Missing Values. Journal of the American Statistical Association, 83(404), 1198-1202. doi:10.1080/01621459.1988.10478722
15. Little, R. J. A., & Rubin, D. B. (1989). The Analysis of Social Science Data with Missing Values. Sociological Methods & Research, 18(2-3), 292-326. doi:10.1177/0049124189018002004
16. Marchenko, Y. (2011). Chained equations and more in multiple imputation in Stata 12. Paper presented at the 2011 Italian Stata Users Group Meeting, Venice, Italy. https://www.stata.com/meeting/italy11/abstracts/italy11_marchenko.pdf
17. Mits ga, M., Ramos, C., & Frias, R. (2011). Ne tworking capability, networking outcomes, and company performance A nomological model including moderation effects.
18. Patrician, P. A. (2002). Multiple imputation for missing data†‡. Research in Nursing & Health, 25(1), 76-84. doi:10.1002/nur.10015
19. Rubin, D. B. (1976). Inference and Missing Data. Biometrika, 63(3), 581-592. doi:10.2307/2335739
20. Rubin, D. B. (1987). Multiple imputation for survey nonresponse. New York: John Wiley and Sons.
21. Schafer, J. L., & Graham, J. W. (2002). Missing data: our view of the state of the art. Psychological Methods, 7(2), 147.
22. Shrive, F. M., Stuart, H., Quan, H., & Ghali, W. A. (2006). Dealing with missing data in a multi-question depression scale: a comparison of imputation methods. BMC Medical Research Methodology, 6(1), 57. doi:10.1186/1471-2288-6-57
23. Tsikriktsis, N. (2005). A review of techniques for treating missing data in OM survey research. Journal of Operations Management, 24(1), 53-62. doi:10.1016/j.jom.2005.03.001
24. Van Buuren, S. (2018). Flexible imputation of missing data (2 ed.). Boca Raton, FL: CRC press.
25. von Hippel, P. T. (2004). Biases in SPSS 12.0 Missing Value Analysis. The American Statistician, 58(2), 160-164. doi:10.1198/0003130043204
26. Wulff, J. N., & Ejlskov, L. (2017). Multiple Imputation by Chained Equations in Praxis: Guidelines and Review. Electronic Journal of Business Research Methods, 15(1), 41-56. Retrieved from https://academic-publishing.org/index.php/ejbrm/article/view/1355
27. Yates, F. (1933). The analysis of replicated experiments when the field results are incomplete. Empire Journal of Experimental Agriculture, 1(2), 129-142.