Een praktische voorbeeldsituatie van een regressieanalyse!
Figuur 1
In de praktijk meten de variabelen welke je hebt verzameld je theoretische construct, maar niet alleen en uitsluitend dat theoretische construct. Als voorbeeld, stel je wil de omvang van een organisatie meten. Welke indicator (proxy) ga je daarvoor selecteren?
Stel we nemen het aantal werknemers. Een redelijke aanname toch? Meer medewerkers betekent een grotere organisatie. Nu gaan we deze aanname eens ontleden. Met aantal medewerkers bedoelen we waarschijnlijk het aantal medewerkers met een voltijds contract. Hierbij moeten we er rekening mee houden dat de organisatie ook gebruik kan maken van parttime medewerkers, uitzendkrachten, oproepkrachten, vrijwilligers, medewerkers op basis van detachering en/of payrolling. Daarom zal het aantal medewerkers hoogstens een indicatie zijn van de organisatieomvang.
Waarom meet een proxy niet “zuiver”?
Als we onze analyse voortzetten kunnen we ons afvragen of het aantal medewerkers alleen en uitsluitend de omvang van de organisatie meet. Zolang we ons beperken tot een groep van organisaties die veel op elkaar lijken is dat waarschijnlijk correct. Maar wat nu als je bijvoorbeeld een softwarebedrijf vergelijkt met een productiebedrijf. Een productiebedrijf heeft doorgaans meer medewerkers nodig om een vergelijkbare economische waarde te creëren.
Kortom, je aantal medewerkers variabele meet niet alleen de grootte van de organisatie (X1) maar ook deels de industrie (X2) waar de organisatie zich in bevindt. Daarnaast is het aannemelijk dat de mate van automatisering of economische ontwikkeling in een land ook een rol kan spelen. Waarschijnlijk heeft het aantal medewerkers ook nog overlap met andere variabelen. Met andere woorden, je aantal medewerkers variabele heeft wat “vervuiling” in zich.
Hoe kan je de onzuivere proxy visualiseren?
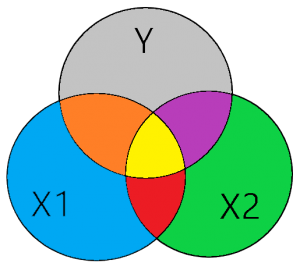
Deze “vervuiling” ofwel gemeenschappelijke variantie met de industrie variabele zal de OLS-regressie uit de omvang variabele (X1) proberen te halen. Zodat alleen die variantie overblijft welke de omvang van de organisatie meet. In figuur 1 zie je dat in het gele gebied zowel X1 als X2 een correlatie (overlap) hebben met Y. Dat gele gebied kan je zien als de “vervuiling”, de “onzuiverheid” van je variabele. De combinatie van het rode en gele gebied in figuur 1 is de gemeenschappelijke variantie (correlatie) tussen variabele X1 en X2. Dit zie je terug als de rho (r) in je correlatiediagram in Stata of SPSS. Heel simpel verwoord, is dit je “vervuiling” van variabele X2 in X1 en visa versa.
Nu ontstaat er een dilemma, hoe gaan we het gele gebied opdelen? Welk deel wijzen we aan de correlatie tussen X1 en Y toe en welk deel wijzen we aan de correlatie tussen X2 en Y toe? Het eerlijke antwoord is, dat we dat niet kunnen bepalen. Simpelweg, we weten het niet. Daarom wordt een rigoureuze maar meest logische beslissing genomen, we verwijderen het gele gebied uit de regressie. Hierdoor wordt het zuivere (unieke) effect van X1 op Y en van X2 op Y gemeten.
Hoe kan je doormiddel van je correlatietabel je regressie analyseren?
De correlatie tussen X1 en Y meet de gemeenschappelijke variatie tussen deze twee variabelen. Doordat X1 een onzuivere proxy is zit er wat vervuiling in deze variabele. Deze vervuiling (gele gebied) wordt door variabele X2 uit variabele X1 gehaald als deze tegelijkertijd in dezelfde regressie worden geanalyseerd. Kortom, het gezuiverde effect X1 op Y wordt in figuur 1 door het oranje gebied verklaard en het gezuiverde effect van X2 op Y wordt door het paarse gebied verklaard.
Op het moment dat we geïnteresseerd zijn in de effecten van X1 (omvang organisatie) op Y bij bepaalde waarden van X2 (industrie), dan praten we over een conditioneel effect ofwel een interactie. Op het moment dat je een interactie in je regressie opneemt voeg je weer het gele gebied aan het model toe.
De regressiecoëfficiënt op basis van je correlatietabel
Op basis van je correlatietabel zou je de gestandaardiseerde beta van je regressietabel kunnen bereken met onderstaande formule (Thompson, 2006, pp. 234-237).
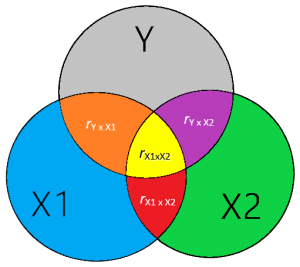
β1 = [ ry*x1 – (ry*x2)*(rx1*x2) ] / [ 1 – rx1*x22]
β2 = [ ry*x2 – (ry*x1)*(rx1*x2) ] / [ 1 – rx1*x22]
Figuur 2
Om bovenstaande formule beter te begrijpen kan deze ook als volgt worden weergegeven.
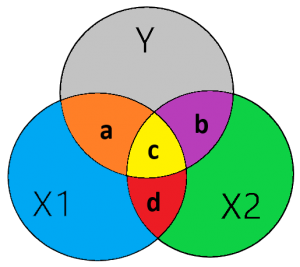
β1 = [a – c] / [ 1 – (c + d)2]
β2 = [b – c] / [ 1 – (c + d)2]
Figuur 3
De standaardfout op basis van je correlatietabel
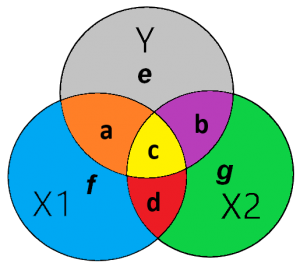
De standaardfout van de regressie kan geïllustreerd worden door het grijze gebied in figuur 4 van Y (e) welke niet verklaard wordt door X1 (a) of X2(b). Met andere woorden, het grijze gebied ( e) is gelijk aan 1- R-squared. Hieruit blijkt dat als er controle variabele(n) wordt (-en) toegevoegd de standaardfout kan worden verkleind. De standaardfout voor X1 kan berekend worden als het onverklaarde gebied van Y (e) gedeeld door de partiële X1 (gebied f + gebied a). Met andere woorden, de standaardfout is het onverklaarde gedeelte van de afhankelijke variabele gedeeld door de unieke variatie van de onafhankelijke variabele.
Figuur 4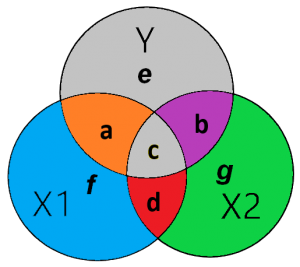
Figuur 5
De standaardfout van de gestandaardiseerde regressie coëfficiënt (O’Brien, 2018):
SE1 = √ [ (e + c) / ((a +f) * (n-k-1))] = √ [1- R2) / ((1 – rx1*x22) * (n-k-1))]
SE2 = √ [ (e + c) / ((b +g) * (n-k-1))] = √ [1- R2) / ((1 – rx1*x22) * (n-k-1))]
De t-waarde van de regressie coëfficiënt (O’Brien, 2018):
t1(n-k-1) = √ [ (a ) / ( [e + c] * (n-k-1)) ] = √ [(1 – rx1*x22) / ((1- R2)*(n-k-1))]
t2(n-k-1) = √ [ (b ) / ( [e + c] * (n-k-1)) ] = √ [(1 – rx1*x22) / ((1- R2)*(n-k-1))]
n = Aantal observaties
k = Aantal onafhankelijke variabelen
Vervolgens zijn er grofweg 3 alternatieve scenario’s te bedenken.
Hierboven hebben we min of meer de ideale omstandigheden besproken als twee onafhankelijke variabelen gemeenschappelijke variatie hebben. Hieronder bekijken we drie extreme scenario’s die in de praktijk kunnen voorkomen.
Scenario 1: Multicollineariteit in een regressieanalyse
Er is multicollineariteit tussen twee of meer variabelen. Multicollineariteit in een regressieanalyse zijn twee of meer variabelen die een hoge mate van samenhang hebben. Hiermee wordt bedoeld dat de overlap tussen X1 en X2 extreme vormen begint aan te nemen. Met andere woorden het effect van variabele X1 op Y lijkt in hoge mate op het effect van variabele X2 op Y. Hierdoor kan de regressieanalyse geen onderscheid meer maken tussen de twee variabelen.
Klik hier voor meer informatie!
Scenario 2: Multicollineariteit & Suppressor effect
Als er naast multicollineariteit ook een suppressor variabele aanwezig is dan heb je te maken met een variabele die (bijna) geen correlatie heeft met je afhankelijke variabele maar wel met een of meer onafhankelijke variabelen. Deze suppressor variabele heeft misschien een negatieve connotatie maar in de statistiek kan een suppressor variabele je regressie juist beter maken. Een suppressor haalt de “vervuilende” variatie uit de andere onafhankelijke variabelen Thompson (2006, pp. 237-238). Hierdoor kan je R-squared en de effect size van je andere onafhankelijke variabelen toenemen Thompson (2006, pp. 237-238). Daarentegen zijn er ook negatieve effecten van een suppressor variabele. Een supressor variabele kan een bron zijn van multicollineariteit en daarmee een oorzaak zijn van grote standaardfouten (type II fout). Daarnaast kan een suppressor zorgen voor onnauwkeurige regressiecoëfficiënten en een bron zijn van onstabiliteit in je regressiemodel (Kidwell & Brown, 1982; Walker, 2003). Kortom, een suppressor variabele heeft voordelen en nadelen.
Klik hier voor meer informatie!
Scenario 3: Omitted Variable Bias
Omitted variable bias (OVB) is een belangrijk controlepunt van je regressieanalyse omdat deze OVB een fundamentele invloed kan hebben op je regressiecoëfficiënt. Als je last hebt van OVB kan je regressiecoëfficiënt een onjuiste waarde aanwijzen. Bijvoorbeeld, je kan een significante positieve beta coëfficiënt meten in je regressie. Maar, deze waarde is in de grotere populatie bijvoorbeeld negatief of niet significant. Kortom, de betrouwbaarheid en validiteit van je regressieanalyse staat ter discussie als je aantoonbare bias hebt.
Klik hier voor meer informatie!
Ben je geïnteresseerd en wil je weten wat wij voor je kunnen beteken? Stel dan vrijblijvend je vraag via ons contactformulier of WhatsApp.
Literatuurlijst
- Kidwell, J. S., & Brown, L. H. (1982). Ridge Regression as a Technique for Analyzing Models with Multicollinearity. Journal of Marriage and Family, 44(2), 287-299.
- O’Brien, R. M. (2018). A consistent and general modified Venn diagram approach that provides insights into regression analysis. PLOS ONE, 13(5), 1-12.
- Thompson, B. (2006). Foundations of Behavioral Statistics: An Insight-Based Approach. New York: Guilford Publications.
- Walker, D. A. (2003). Suppressor Variable(s) Importance within a Regression Model: An Example of Salary Compression from Career Services. Journal of College Student Development, 44(1).